Hold The Block

Classical Mechanics Level 4

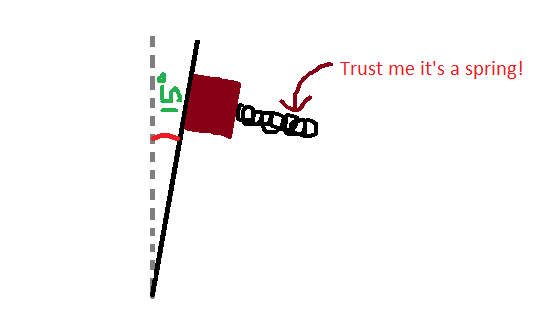
A wall is tilted by 1 5 ∘ 15^\circ (with vertical axis), and a 2 kg 2 \text{ kg} block is placed against the wall. The block is held in place with a spring (Spring is pushing the block towards the wall). The coefficient of friction between the block and the wall is μ s = 0.61 \mu_{s} = 0.61 . Holding the block in place requires that the spring be compressed by 12 cm 12\text{ cm} . What is the spring constant of the spring in N/m \text{N/m} ?

Take g = 9.8 ms − 2 g = 9.8\text{ ms}^{-2} .


The answer is 301.

Farhabi Mojib by Farhabi Mojib , 23, Bangladesh

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Farhabi Mojib
Jan 4, 2017

Here normal force N = f s p r i n g − m g sin ⁡ θ N = f_{spring} - mg \sin \theta
And m g cos ⁡ θ mg \cos \theta is component of gravitational force on the block parallel to the surface of the wall.
So to hold the block friction force on the block must be equal (or greater) to m g cos ⁡ θ mg \cos \theta .
We know maximum friction force f = μ s N f=\mu_{s}N
So,
μ s ( f s p r i n g − m g sin ⁡ θ ) = m g cos ⁡ θ \mu_{s} (f_{spring} - mg \sin \theta) = mg \cos \theta
Which implies f s p r i n g = m g sin ⁡ θ + m g cos ⁡ θ μ s f_{spring} = mg \sin \theta + \frac{mg \cos \theta}{\mu_{s}}
And f s p r i n g = k x f_{spring} = kx
So,
k = m g x ( sin ⁡ θ + cos ⁡ θ μ s ) k = \frac{mg}{x} (\sin \theta + \frac{\cos \theta}{\mu_{s}})
=300.909
Rounding this we get 301 \boxed{301} .


1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...