Hold your bike, Beki!

Classical Mechanics Level 3

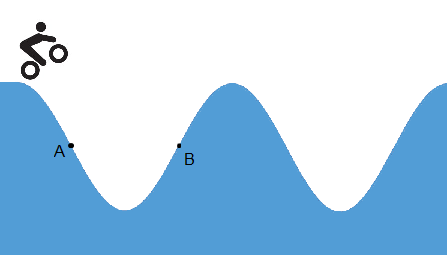In a rainy day, Beki rides her faulty mountain bicycle on an irregular terrain. When she achieves a certain velocity, the bike starts shaking and breaks. She realizes the problem is resonance. She goes home and fixes the bike. The next day, a sunny one, she goes to the same place again and rides faster than the day before to avoid resonance. But, as before, the bike trembles again and breaks. Calculate the sum of the velocities in the rainy and the sunny days in Km/h.

Details and Assumptions

  1. The distance between A and B is 25 cm

  2. Temperature of the rainy day: 290 K

  3. Temperature of the sunny day: 300 K

  4. Assume the resonance frequency varies with the temperature due to dilatation and follows this function: f ( T ) = [ 1 9 × T { K } − 260 9 ] { H z } f(T)=\left[ \frac { 1 }{ 9 } \times \frac { T }{ \left\{ K \right\} } -\frac { 260 }{ 9 } \right] \left\{ Hz \right\}

f is the resonance frequency. The K and Hz in braces are just for the dimension to be correct.

This problem was inspired in something my teacher said and in this site: Resonance and Damping


The answer is 14.

View wiki
Diego Barreto by Diego Barreto , 23, Brazil

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Diego Barreto
Feb 8, 2015

1) The wave length of the wave associated with this movement is 2xAB=2x25 cm. Therefore, λ = 0.5 m \lambda =0.5m

2) In the rainy day: f ( 290 ) = [ 1 9 × 290 K { K } − 260 9 ] { H z } = 30 9 H z f(290)=\left[ \frac { 1 }{ 9 } \times \frac { 290K }{ \left\{ K \right\} } -\frac { 260 }{ 9 } \right] \left\{ Hz \right\} =\frac { 30 }{ 9 } Hz

The velocity which Beki travels in the rainy day is V R D = 0.5 × 30 9 m / s = 5 3 m / s { V }_{ RD }=0.5\times \frac { 30 }{ 9 } m/s=\frac { 5 }{ 3 } m/s V R D = 6 K m / h \boxed{{ V }_{ RD }=6 Km/h}

3) In the sunny day: f ( 300 ) = [ 1 9 × 300 K { K } − 260 9 ] { H z } = 40 9 H z f(300)=\left[ \frac { 1 }{ 9 } \times \frac { 300K }{ \left\{ K \right\} } -\frac { 260 }{ 9 } \right] \left\{ Hz \right\} =\frac { 40 }{ 9 } Hz

The velocity which Beki travels in the sunny day is V S D = 0.5 × 40 9 m / s = 20 9 m / s { V }_{ SD }=0.5\times \frac { 40 }{ 9 } m/s=\frac { 20 }{ 9 } m/s V S D = 8 K m / h \boxed{{ V }_{ SD }=8 Km/h}

4) Therefore, the answer is 6+8 = 14 \boxed{14}

(For those who didn't got it Beki is an anagram of Bike).

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...