Hold your ground.
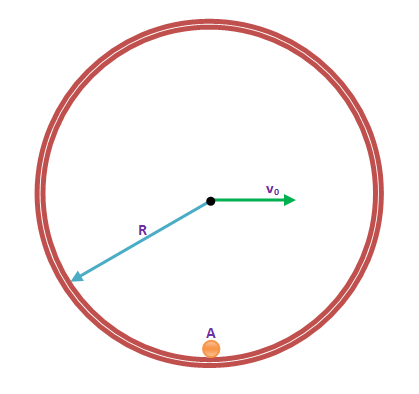 A small body A is fixed to the inner side of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane. At the moments when the body A gets into the lower position, the centre of the hoop moves with velocity
. The maximum value of
at which the hoop moves without bouncing is
. What is the value of
?
A small body A is fixed to the inner side of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane. At the moments when the body A gets into the lower position, the centre of the hoop moves with velocity
. The maximum value of
at which the hoop moves without bouncing is
. What is the value of
?
Try more from my set Classical Mechanics Problems .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The tendency of jumping of hoop will be maximum when the body A is at top most position.
Let at this position the linear velocity of hoop is V . So, velocity of the body is 2 V .
Now for hoop to jump, Centrifugal force given by the body on hoop must be greater than weight of the combined system.
So, F c p = R m V 2 = 2 m g (Here in F c p only V is taken into account and not 2 V because the velocity of body A relative to the centre of mass of hoop is V )
or, V = 2 g R
Since there is no energy loss, so we can use conservation of energy.
So, 2 1 I c m w i 2 + 2 1 ( 2 m ) v c m i 2 = ( 2 m ) g R + 2 1 I c m w f 2 + 2 1 ( 2 m ) v c m f 2
Therefore 2 1 2 R 2 3 m R 2 V o 2 + 4 m V o 2 = 2 m g R + 2 1 2 R 2 3 m R 2 V 2 + m ( 2 3 V ) 2 [Here v c m i = 2 V o & v c m f = 2 3 V ]
or, m V o 2 = 2 m g R + 3 m V 2
or, V o 2 = 2 g R + 3 V 2
Now putting the value of V = 2 g R in above equation
V o 2 = 2 g R + 3 ( 2 g R )
or, V o 2 = 8 g R
or, V o = 8 g R .
So to prevent hoop from jumping V o must be less than or equal to 8 g R .