Hole in the Wall!
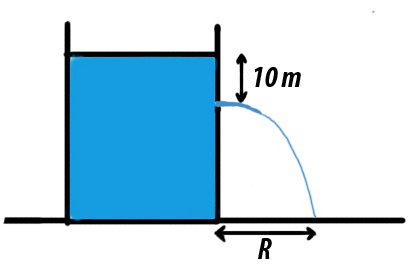 A large tank is filled with water (density
ρ
). A small hole is made at a depth of
h
=
1
0
m
below the water surface. The range of water issuing out of the hole is
R
on ground. What
Extra Pressure
(in atm) must be applied on the water surface so that the range becomes
2
R
?
A large tank is filled with water (density
ρ
). A small hole is made at a depth of
h
=
1
0
m
below the water surface. The range of water issuing out of the hole is
R
on ground. What
Extra Pressure
(in atm) must be applied on the water surface so that the range becomes
2
R
?
Details and Assumptions:
∙
The answer to this problem is an
Integer
∙
ρ
=
1
0
3
k
g
/
m
3
∙
g
=
1
0
m
/
s
2
∙
Water is assumed to be
ideal
liquid
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Firstly, we need to calculate the velocity of the water that gushes out of the small hole at 1 0 m from the water surface to reach the range of R . This can be done so, using Torricelli equation which is...
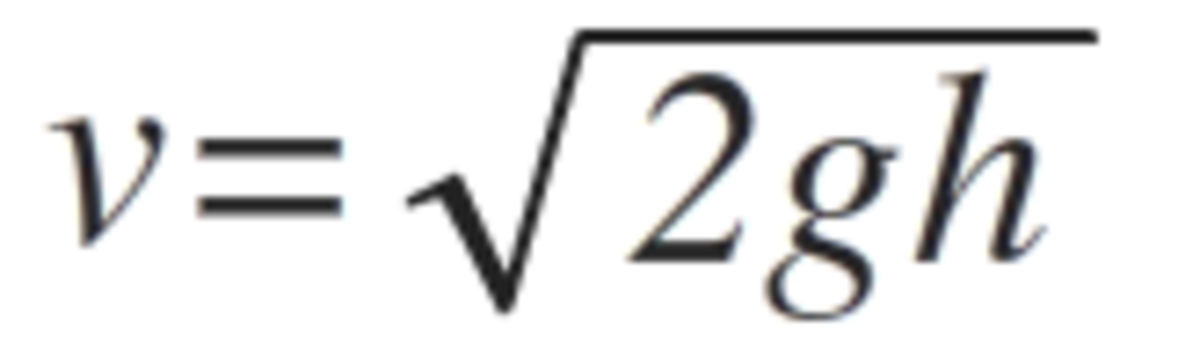
In order to travel twice the range, which is 2 R , the velocity must also be doubled. Hence, using the previously calculated velocity, double it and equate that value with Torricelli equation again to find the new depth of the water from the surface.
Now, be careful , the question asks for the extra pressure, which implies the extra height of the water from its surface. Hence, you would need to substract the old depth from the new depth to find the change in height and it should yield 3 0 m . Finally, use...
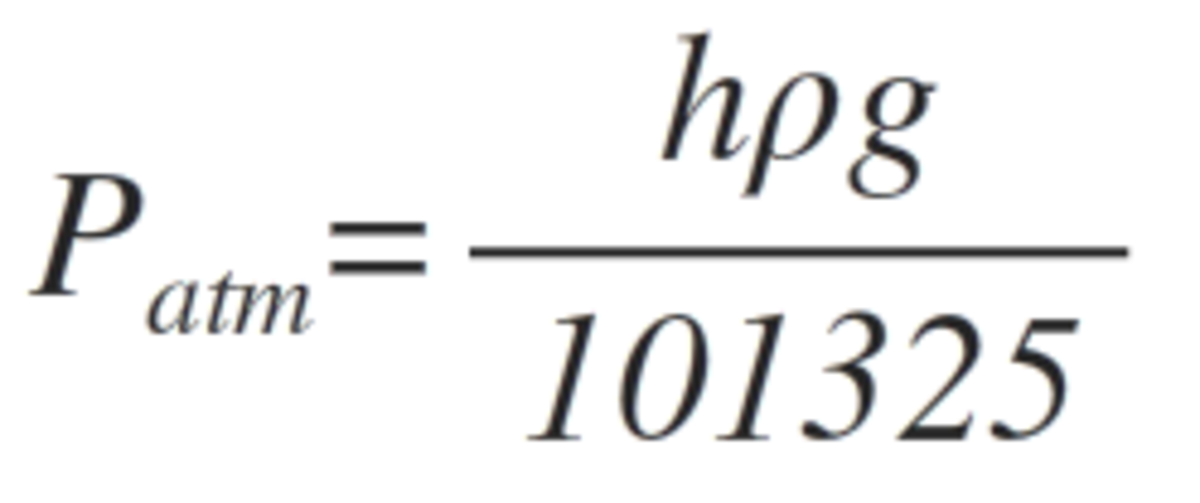
to find the required pressure in a t m and approximate that value to 3 , which is the answer!
Let the
speed
with which the water rushes out be
v
and the
height
of the tank be
ℓ
.
Then, applying fundamental Kinematics equations,
Clearly,
( ℓ − 1 0 ) = 2 1 g t 2 and R = v t
Eliminating t , we get,
R = v g 2 ( ℓ − 1 0 )
It is obvious that, to double the Range, we have to double the speed with which the water ejects.
Now,
Taking the origin at the bottom of the tank,
Assume
P
to be the
Extra Pressure
that we apply and
P
o
to be the atmospheric pressure.
Also, as the tank is
large
, we can consider the velocity of water at the surface to be
zero
.
Applying Bernoulli's Equation , taking the streamline to start at the surface and ending just outside the hole, for the initial case, as well as the final case, we get,
P o + ρ g ℓ = P o + ρ g ( ℓ − 1 0 ) + 2 1 ρ v 2 , and
( P o + P ) + ρ g ℓ = P o + ρ g ( ℓ − 1 0 ) + 2 1 ρ ( 2 v ) 2
Simplifying the two equations, we get,
ρ g ( 1 0 ) = 2 1 ρ v 2 , and
P + ρ g ( 1 0 ) = 2 ρ v 2
Solving, we get,
P = 3 ρ g ( 1 0 )
⇒ P = 3 0 0 0 0 0 P a
⇒ P ≈ 3 atm
Hey, I have a question. While writing Bernoulli's equation, you (and all books too) take the pressure at the hole as the atmospheric pressure. Why should it be so? Shouldn't we be considering the pressure of the water over there? The atmospheric pressure is the pressure outside the hole. Also, I don't see any reason why it should equal the pressure of the water at that level (unless we're talking about hydro statics ). Approximation?
Parth: so the thing is, P initial is on top of the container.... and the second P is pressure just outside the hole. Since, both of those points are exposed to only atmospheric pressure, their value is same. Now if the tank was closed from top, then those values might not be the same.
Hi , I wanted to know if we take surface of water as base line for potential energy , then while writing potential energy of the hole we have to give it a negative sign or positive sign .
FOR DOUBLE RANGE EFFLUX VELOCITY SHOULD BE 2 TIMES USE BERNOULLI'S EQUATION
To Double the Range,we will have to double the velocity of efflux
Let the initial velocity of efflux of water be v
then final velocity of efflux is 2 v
Let P 1 be the EXTRA PRESSURE required and P o be the atmospheric pressure
Applying Bernoulli's Equation(taking potential energy reference at height 10 metres below water level)
also velocity at top of the tank is negligible since A v t o p = a v ⇒ v t o p = A a v . . . a n d A > > a
making the equations for the two cases..we get
P o + ρ g ( 1 0 ) = P o + 2 1 ρ ( v ) 2
( P 1 + P o ) + ρ g ( 1 0 ) = P o + 2 1 ρ ( 2 v ) 2
On Solving...we get
P 1 = 3 × 1 0 ρ g
⇒ P 1 = 3 a t m ( a p p r o x . )