Holy Mountain!
Geometry
Level
1
Determine the height of a mountain if the elevation of its top at the unknown distance from its base is 30Degree and at the distance 10km further off from the mountain, along the same line, angle of elevation is 15Degree.
21
5
19
9
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
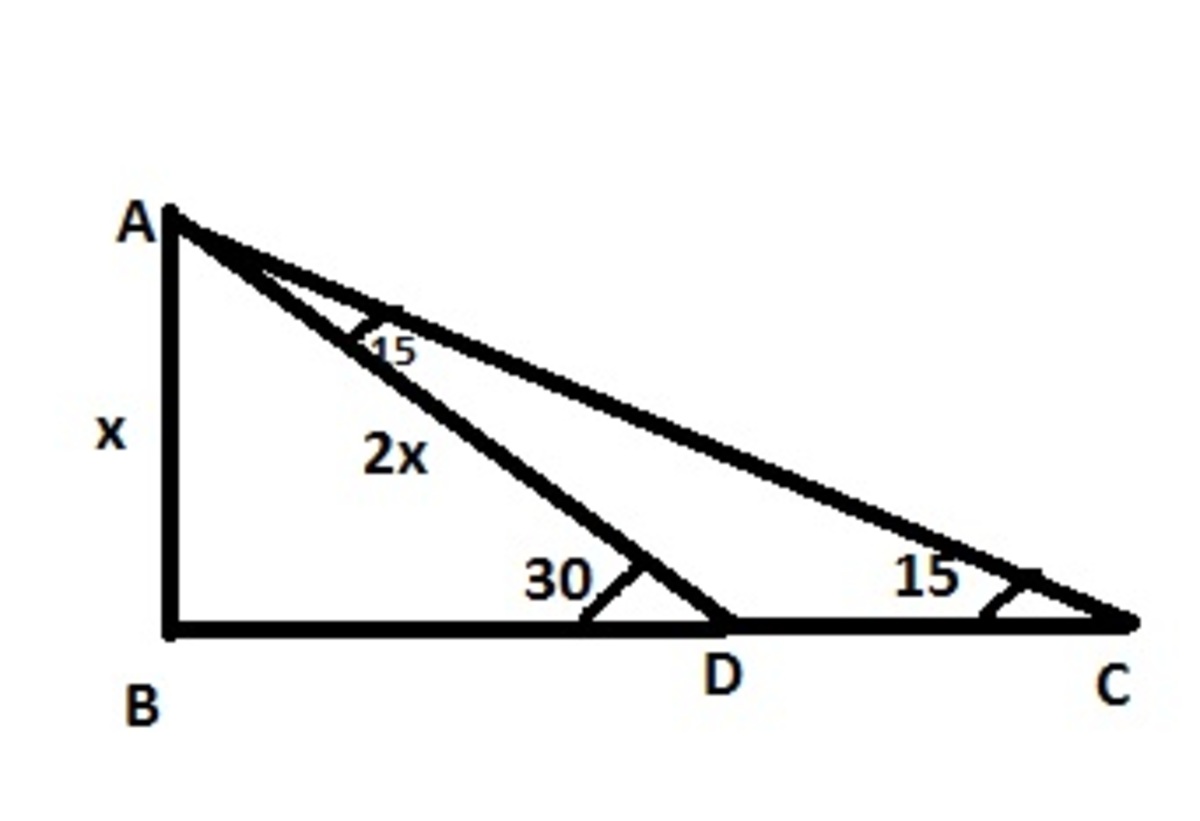Let the height of the mountain, AB be x. Angle D is 30 degree. sin30 = 1/2. So, AD = 2x. Angle C is 15 degree. So, by applying exterior angle property, angle DAC = 15 degree. So, AD = DC. DC = 2x = 10km. So, x = 5km which is the height of the mountain.