Home Sweet Home
 Bill & Bob are building a new house for their dog, Lyca. Bill alone can finish building in 3 hours while Bob is more delicate and can complete the same task alone in 6 hours.
Bill & Bob are building a new house for their dog, Lyca. Bill alone can finish building in 3 hours while Bob is more delicate and can complete the same task alone in 6 hours.
How many hours does it take for both of them to build Lyca's house?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Recall:
Rate x Time = Distance
We can use this formula, but substitute Job for Distance:
Rate x Time = Job
Set Job = 1
Therefore the equation simplifies to:
Rate x Time = 1
Bill can do the job in 3 hours so the equation for Bill is:
R x 3 = 1
Solve for R
Bill's rate is: R = 3 1
Similarly, we can find Bob's rate like so:
R x 6 = 1
Solve for R
Bob's rate is: R = 6 1
Combine the both rates:
3 1 + 6 1 = 2 1
Their combined rate is: 2 1
Use Formula again:
R x T = 1
2 1 x T = 1
T = 2
Working at the same time, in 6 hours they would build 3 houses (Bill 2 and Bob 1) Therefore it will take 6/3 or 2 hours to build one.
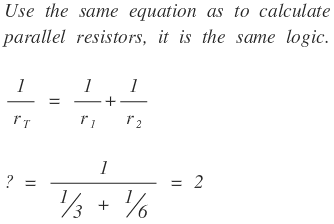
In 1 hour, Bill completes 1/3 of the whole work, and Bob completes 1/6 in an hour.
Thus, if they work together, they will complete 1/3+1/6 = 1/2 of the whole work in an hour.
So it will take 1/(1/2) = 2 hours to build Lyca's house.