Hop on over
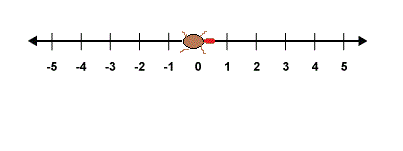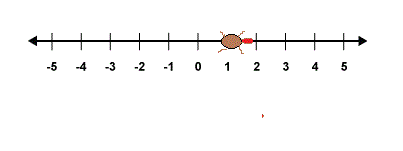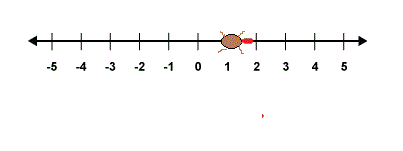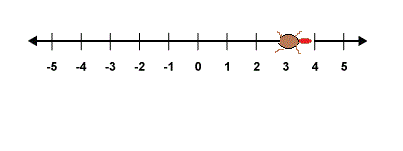 Brilli the bug is constrained to move on a number line ranging
. It starts at 0 and can go either left or right but moves in a way such that the
th 's move it takes
steps.
Brilli the bug is constrained to move on a number line ranging
. It starts at 0 and can go either left or right but moves in a way such that the
th 's move it takes
steps.
What is the minimum number of moves required to reach 32 on the number line.
Details and Assumptions :
-
As an explicit example to reach position it takes a minimum of moves
-
The -th move can be done with as a combination of left and right movement
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 2 = 1 − 2 + 3 + 4 + 5 + 6 + 7 + 8