Hopping to the Right
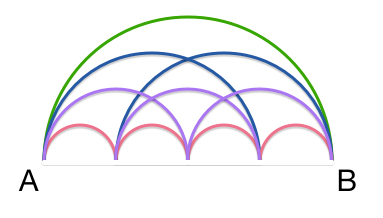
How many ways are there to get from A to B if we are only allowed to move to the right along the colored semicircle arcs?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Essentially, you can get to any point from any previous point. So, the number of ways to get to any point is given by the sum of the ways to get to any of the previous points.
So, if n m = The number of ways to get to the m th point.
Then n m = ∑ i < m n i
And clearly n 1 = 1 and n 2 = 1
Therefore,
- n 1 = 1
- n 2 = 1
- n 3 = 2
- n 4 = 4
n 5 = 8
Oh, it's actually much easier / more direct than that. There's a reason why the answer is listed as 2 3 = 8 .
If you look at the numbers you generated, they are all powers of 2.
Log in to reply
True.
Trusting patterns though, and what things look like can often be misleading...
Aren't 1,1,2,4 and 8 tetranacci numbers ?
There are 3 intermediate steps between A and B. For each step, we either land there or do not land there.
Once we know which steps we land on, there is a unique way to get from A to B (basically taking the arc to the next step). This sets up the bijection between ways from A to B and the set of steps that we land on.
Hence, there are 2 3 ways to get from A to B.
We see that this solution easily generalizes to get 2 n ways from A to B (where n is the number of intermediate steps).