Horace and School Conditional Probability (Part II)

Probability Level 1

Horace turns up at school either late or on time. He is then either shouted at or not. The probability that he turns up late is $0.4.$ If he turns up late, the probability that he is shouted at is $0.7$ . If he turns up on time, the probability that he is still shouted at for no particular reason is $0.2$ .

You hear Horace being shouted at. What is the probability that he was late?

This problem is not original.

The answer is 0.7.

5 solutions

Brian Charlesworth
Feb 15, 2015

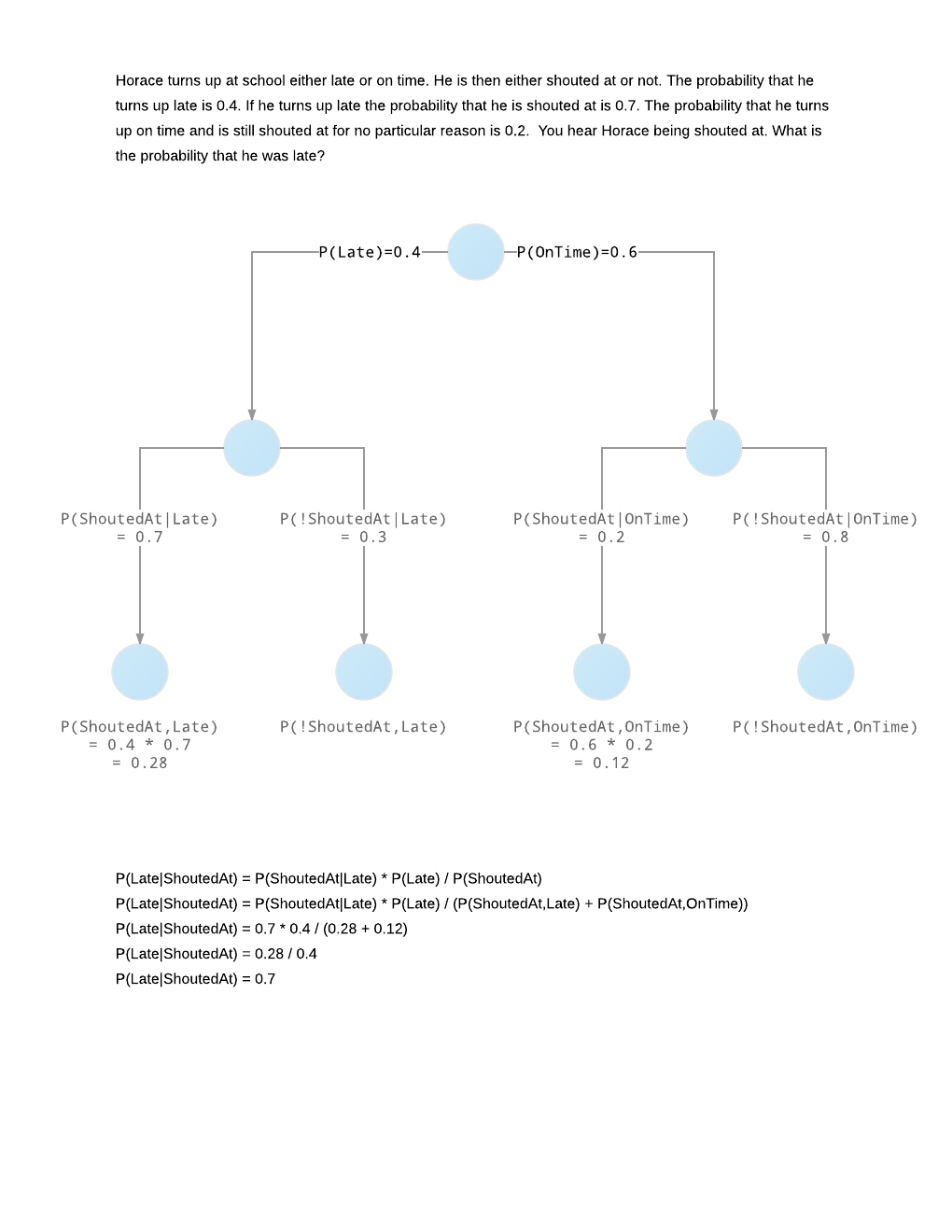
Let $A$ be the event that Horace turns up late and $B$ be the event that he gets shouted at. We must then calculate the probability that he was late given that he is shouted at. This will be

$P(A | B) = \dfrac{P(A \cap B)}{P(B)}.$

Now $P(A \cap B) = P(A) * P(B | A) = (0.4)(0.7) = 0.28.$

Next, $P(B) = P(B \cap A) + P(B \cap \overline{A}) = (0.4)(0.7) + (1 - 0.4)(0.2) = 0.4.$

Thus $P(A | B) = \dfrac{0.28}{0.4} = \boxed{0.7}$ .

There is a mistake.

P(B * !A) is NOT (1- 0.4)(0.2) According to the statement of the problem, it is .2 : "The probability that he turns up on time AND is still shouted at for no particular reason is .2 "

Daniel Lalonde - 2 years, 11 months ago

Your interpretation is correct. I'm not sure if the wording was (incorrectly) changed at some point; I believe that the original intent was to have the condition that if Horace turns up on time then he is shouted at with probability $0.2$ . Given the number of solvers and solutions posted I suggest that, rather than having the posted answer updated or the question deleted, I change the wording to reflect what I sense was it's original intent, (I am a moderator, which gives me the ability to do that). Is that ok? We could also ask staff to consider updating the answer to what you calculated, (which would invalidate the posted solutions), or at least give you credit for a correct answer while changing the wording as I have suggested.

Brian Charlesworth - 2 years, 11 months ago

Sam Khavari
May 20, 2016

Here is an overly detailed explanation of the solution

The problem does not state: "P of being shouted at WHEN on time is .2" The question states : "P of being on time AND shouted at is .2" (In other words, P(ShoutedAt|On Time) really is .2/.6=0.33 . , not 0.2 ; and P(ShoutedAt, OnTime) really is 0.2 , as in the problem's statement) Ergo, the answer should be .28/(.2+.28)= .28/.48= .583

Daniel Lalonde - 2 years, 11 months ago

Hamlet Sentit
Feb 15, 2015

Baeyes theorem

Divyansh Chaturvedi
Feb 20, 2015

Bro u asked the same question about which u have informed in the q...

Srinivas Vijay Babu
Nov 18, 2020

Let A be the probability of him getting shouted at. Let B be the Probability of him being late. Then, P( A|B ) = $\frac{P( B|A ) * P(A)}{P(B)}$ by Bayes' theorem Now, we know everything to solve this equation except for P(A). To solve it, we know that the probability of him getting shouted at if he turns up late is 0.7. And we know that the probability of him turning up late is 0.4. We can just multiply to get, 0.7 0.4 = 0.28 Additionally, we know that the probability of him turning up on time and getting shouted at is 0.2, and we know that the probability of him being late is 0.4 so he being on time is 0.6. So we multiply, 0.6 0.2 and get 0.12. So 0.28 + 0.12 is 0.4 so (0.7 x 0.4)/0.4 = 0.7

Horace and School Conditional Probability (Part II)

This problem is not original.

The answer is 0.7.

5 solutions

0 pending reports