Horizontal projection

Classical Mechanics Level 3

A stone is thrown at a speed of 19.6 m/sec at an angle 30 degrees above the horizontal from a tower of height 490 meter. Find the time during which the stone will be in air.


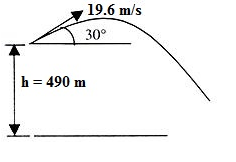
The answer is 11.05.

Swaraj Shandilya by Swaraj Shandilya , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

We can use the formula y = V o y t − 1 2 g t 2 y=V_{oy} t-\dfrac{1}{2}g t^2 where y = − 490 y=-490 , V o y = sin ⁡ 3 0 ∘ ( 19.6 ) V_{oy}=\sin 30^\circ(19.6) and g = 9.81 g=9.81 .

Substitute:

− 490 = sin ⁡ 30 ( 19.6 ) t − 1 2 ( 9.81 ) t 2 -490=\sin 30 (19.6)t - \dfrac{1}{2}(9.81)t^2

− 490 = 9.8 t − 4.905 t 2 -490=9.8t-4.905t^2

4.905 t 2 − 9.8 t − 490 4.905t^2-9.8t-490

Use the quadratic formula to solve for t t .

t = − b ± b 2 − 4 a c 2 a = 9.8 ± ( − 9.8 ) 2 − 4 ( 4.905 ) ( − 490 ) 2 ( 4.905 ) = 980 981 ± 9709.84 9.81 ≈ 11.043682 seconds t=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}=\dfrac{9.8 \pm \sqrt{(-9.8)^2-4(4.905)(-490)}}{2(4.905)}=\dfrac{980}{981}\pm \dfrac{\sqrt{9709.84}}{9.81} \approx \boxed{\color{#69047E}11.043682~\text{seconds}}

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Swaraj Shandilya
Jun 22, 2015

Vertical motion (downward direction negative) :

Initial vertical velocity y = 19.6 sin 30o

Acceleration a = g = -9.8 m/s2

Vertical distance covered = h = 490 m

Using, h = ut + 1/2gt2

We have, 490 = - 9.8t + (1/2) 9.8t2

100 = - 2t + t2 or t2 - 2t - 100 = 0

t = \frac{2\pm \sqrt{(2^{2}-4\times 1\times \left [ -100 \right ])}}{2\times 1} =1+\sqrt{101}

t = 11.05 sec

0 Helpful 0 Interesting 0 Brilliant 0 Confused

I've done the LaTeX job for you. So you can correct your math typing by copy-pasting my codes!

Vertical motion (downward direction negative) : Initial vertical velocity y = 19.6 s i n 3 0 0 y = 19.6 sin 30^0 Acceleration a = g = − 9.8 m / s 2 a = g = -9.8 m/s^2 Vertical distance covered = h = 490 m = h = 490 m Using, h = u t + 1 2 g t 2 h = ut + \frac{1}{2} gt^2 We have, 490 = − 9.8 t + 1 2 9.8 × t 2 490 = - 9.8t + \frac{1}{2} 9.8 \times t^2 100 = − 2 t + t 2 100 = - 2t + t^2 o r , t 2 − 2 t − 100 = 0 or, t^2 - 2t - 100 = 0 t = 2 ± ( 2 2 − 4 × 1 × [ − 100 ] ) 2 × 1 = 1 + 101 t = \frac{2 \pm \sqrt{(2^{2}-4\times 1\times \left [ -100 \right ])}}{2\times 1} =1+\sqrt{101} t = 11.05 s e c t = 11.05 sec

Muhammad Arifur Rahman - 5 years, 11 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...