Horizontal Shot

Classical Mechanics Level 4

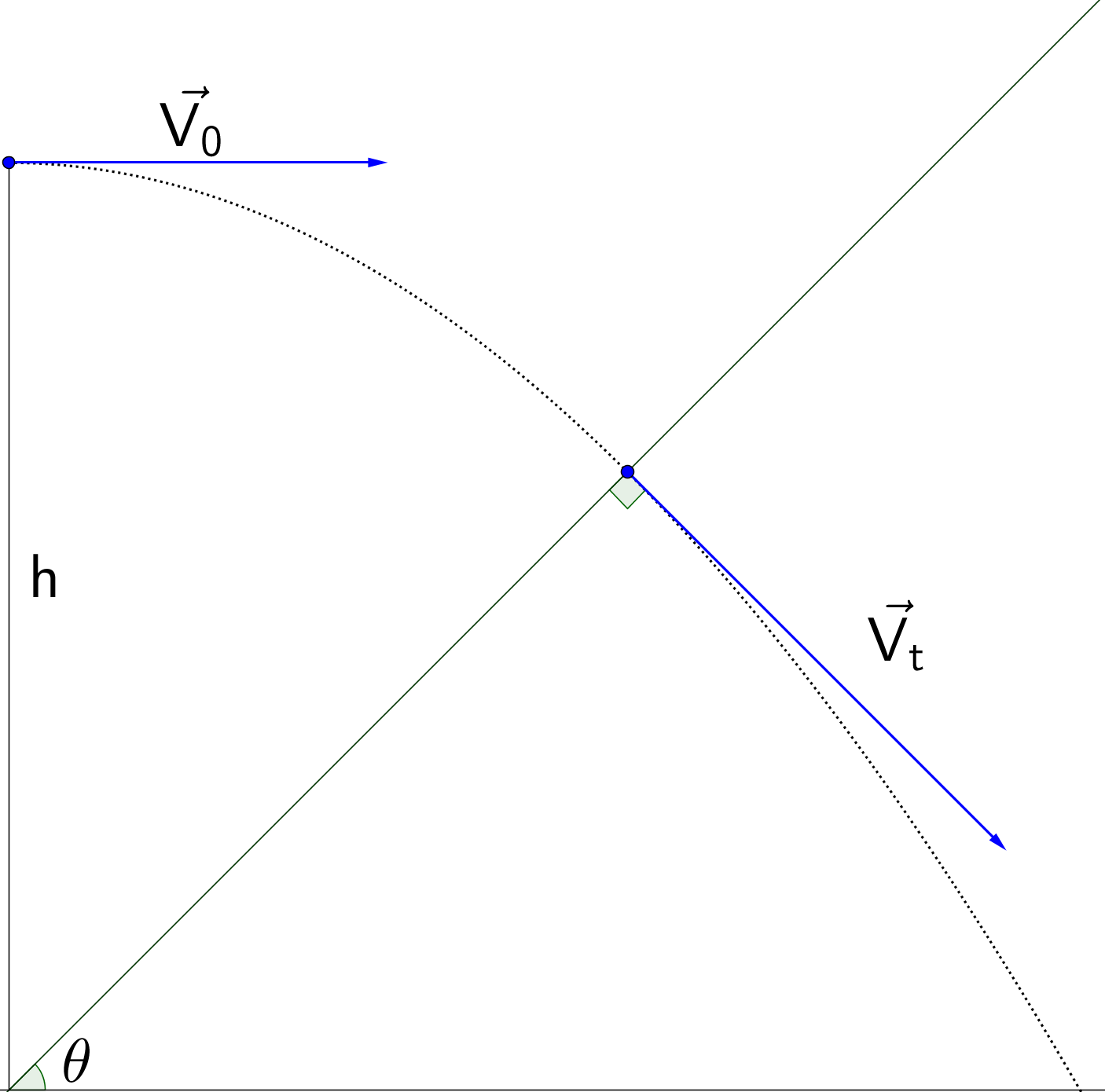
A particle is thrown horizontally from a height h h with initial velocity V 0 V_0 . It hits a plane inclined with an angle θ \theta with respect to the horizontal. What is the value of V 0 V_0 such that the particle hits the plane perpendicularly?

V 0 = sin ⁡ θ 2 g h cos ⁡ 2 θ + 1 V_0=\dfrac{\sin\theta \sqrt{2gh}}{\sqrt{\cos^2 \theta+1}} V 0 = cos ⁡ θ 2 g h cos ⁡ 2 θ + 1 V_0=\dfrac{\cos\theta \sqrt{2gh}}{\sqrt{\cos^2 \theta+1}} V 0 = sin ⁡ θ 2 g h sin ⁡ 2 θ + 1 V_0=\dfrac{\sin\theta \sqrt{2gh}}{\sqrt{\sin^2 \theta+1}} V 0 = cos ⁡ θ 2 g h sin ⁡ 2 θ + 1 V_0=\dfrac{\cos\theta \sqrt{2gh}}{\sqrt{\sin^2 \theta+1}}

View wiki
Alan Enrique Ontiveros Salazar by Alan Enrique Ontiveros S… , 22

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Michael Mendrin
Apr 15, 2016

Given parameters g g , h h , and V 0 {V}_{0} , the equation of the trajectory can be described as follows

y = h − 1 2 g V 0 2 x 2 y=h-\dfrac { 1 }{ 2 } \dfrac { g }{ { {V}_{0} }^{ 2 } } { x }^{ 2 }

The equation of any normal passing through the trajectory point where x = x 0 x={x}_{0} is then

V 0 2 g x 0 ( x − x 0 ) + h − 1 2 g V 0 2 x 0 2 \dfrac { { {V}_{0} }^{ 2 } }{ g{ x }_{ 0 } } \left( x-{ x }_{ 0 } \right) +h-\dfrac { 1 }{ 2 } \dfrac {g }{ { {V}_{0} }^{ 2 } } { { x }_{ 0 } }^{ 2 }

where, for this problem, we are looking for the normal that passes through the origin ( 0 , 0 ) \left(0,0\right) , so upon solving, we find that

x 0 = 2 V 0 g g h − V 0 2 { x }_{ 0 }=\dfrac { \sqrt { 2 } {V}_{0} }{ g } \sqrt { gh-{ {V}_{0} }^{ 2 } }

So using the original equation for the trajectory, we can find the tangent of the slope as a function of g , h , V 0 g, h, {V}_{0} , which we shall equate with T a n ( θ ) Tan(\theta)

V 0 2 g h − V 0 2 = T a n ( θ ) \dfrac { { V }_{ 0 } }{\sqrt{2} \sqrt { gh-{{V}_{ 0}}^{ 2 } } } =Tan\left( \theta \right)

Solving for V 0 {V}_{0} eventually gets us

V 0 = S i n ( θ ) 2 g h S i n 2 ( θ ) + 1 { V }_{ 0 }=\dfrac { Sin\left( \theta \right) \sqrt { 2gh } }{ \sqrt { {Sin}^{2} \left( \theta \right) +1 } }

9 Helpful 1 Interesting 1 Brilliant 0 Confused

I agree with you up to V o 2 g h − V o = tan ⁡ θ \frac{V_o}{\sqrt{2} \sqrt{gh-V_o}}=\tan \theta But after squaring and grouping you get V o 2 ( 1 + 2 tan ⁡ 2 θ ) = 2 g h V_o^2(1+2\tan^2 \theta)=2gh Which is almost obvious to notice that equals V o 2 sec ⁡ 2 θ ( sin ⁡ 2 θ + 1 ) = 2 g h V_o^2 \sec^2 \theta(\sin^2 \theta +1)=2gh Which finally yielss V o = cos ⁡ θ 2 g h sin ⁡ 2 θ + 1 V_o=\frac{\cos \theta \sqrt{2gh}}{\sqrt{\sin^2 \theta +1}}

Erasmo Hinojosa - 5 years, 1 month ago

Log in to reply

Maybe you should double check your calculations, particularly "after grouping you get"? I get a different result.

Michael Mendrin - 5 years, 1 month ago

Log in to reply

I missed a tan ⁡ 2 θ \tan^2 \theta Thank you!

Erasmo Hinojosa - 5 years, 1 month ago
Winston Cahya
Jun 6, 2016

I solved it by changing coordinates and the putting Vx=0.Is this method possible ?

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...