Horrible Hexagons 1
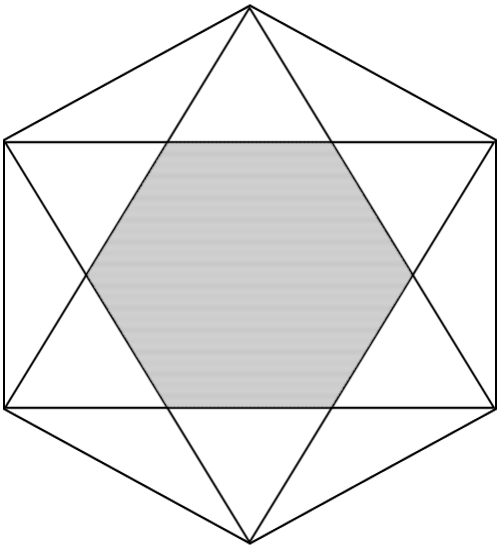 The diagram above shows a regular hexagon
with two equilateral triangles inscribed in it.
The diagram above shows a regular hexagon
with two equilateral triangles inscribed in it.
If the shaded region has area , what is the area of in terms of ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Method 1:
Each of the 1 2 "distinct" triangles encircling the shaded region have the same area, and the shaded region can be formed by "folding" the 6 of these triangles that are equilateral about the sides they share with the shaded region. In this way we see that H 1 is composed of 1 8 non-overlapping triangles of the same area, and thus H 1 = 6 1 8 x = 3 x units 2 .
Method 2:
By symmetry we see that the shaded area is a regular hexagon with side lengths that are 2 1 sec ( 3 0 ∘ ) = 3 1 that of side lengths of H 1 . Since the area of a regular hexagon is proportional to the square of the length of its sides, we see that the area of the shaded region is ( 3 1 ) 2 = 3 1 that of H 1 , and hence the area of H 1 is 3 x units 2 .