Horsin around
In this chessboard, considering that the knight cannot walk into the black squares, what is the minimum number of steps it needs to go from a1 to c7?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Você é brasileiro? No xadrez em inglês a peça do cavalo é chamado de cavaleiro (Knight). Só uma observação. Aliás, bom problema.
Log in to reply
Vish, agora que eu vi que eu coloquei errado no problema também né, valeu por me mostrar. No título era só como um trocadilho mesmo por conta do desenho do (Knight) ser um cavalo mesmo não tendo esse nome no inglês mas valeu mesmo assim.
This should be a logic problem.
Log in to reply
Works by logic too, that's a good thing about this problem. What you do by logic is the same as what you do on the breadth-first search algorithm and the example is small enough that you can work it by hand but at the same time it should give you some intuition on how the algorithm works. I really liked your answer, but now I challenge you, can you generalize the problem for, given an arbitrary start position, how you can reach an arbitrary end position?
It can be approached by an algorithm, however, this is much more time consuming. I always prefer a more simple and shorter proof, and I feel that a solution such as mine (see below/above) is more elegant (which is done by logic).
can someone do this in python?
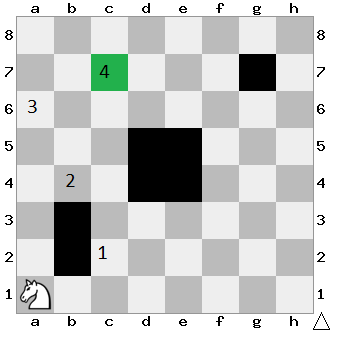
Solution: 4 moves.
Reason: The first valid move for the white knight must be c2. After c2, the knight should move to b4 or e3 or e1. If the knight moves to e3 and e1, it must take more than 4 moves to reach c7. So the knight should move to b4. After b4, the knight should move either a6 or c6. We observe that if the knight moves to a6, it takes just 2 moves to reach c7 from b4. So the knight should move to a6.
Hence the minimum number of moves required for the knight to reach a7 is 4.
I just want to write another answer A1→C2→A3→B5→C7
We can find a solution in 4 steps: A1 → C2 → B4 → A6 → C7. Now we just need to prove it is the shortest.
The knight starts on a black square, and has to get to a black square. Since, each move alternates the colour, it will take an even number of moves. 2 moves is clearly not possible just by looking at it (even ignoring the squares that it can't pass through) but if you want a more rigorous approach you can use Pythagoras. Therefore, 4 is the lower bound, and it is possible, so it is the answer.
We can think of the board as a graph where every node is a position on the board and every edge is a possible move from one position to another. Then one can apply the breadth-first search algorithm to find the shortest path. Here is my c++11 implementation on an implicit graph.
and here is one path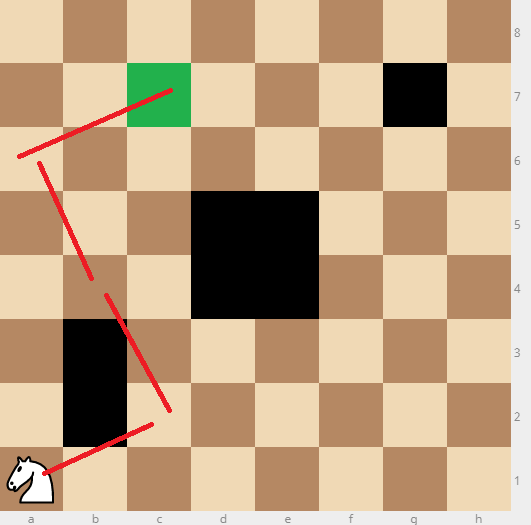
As by request, I've added a python version, I also added more comments to hopefully help