Hosam's Incircles
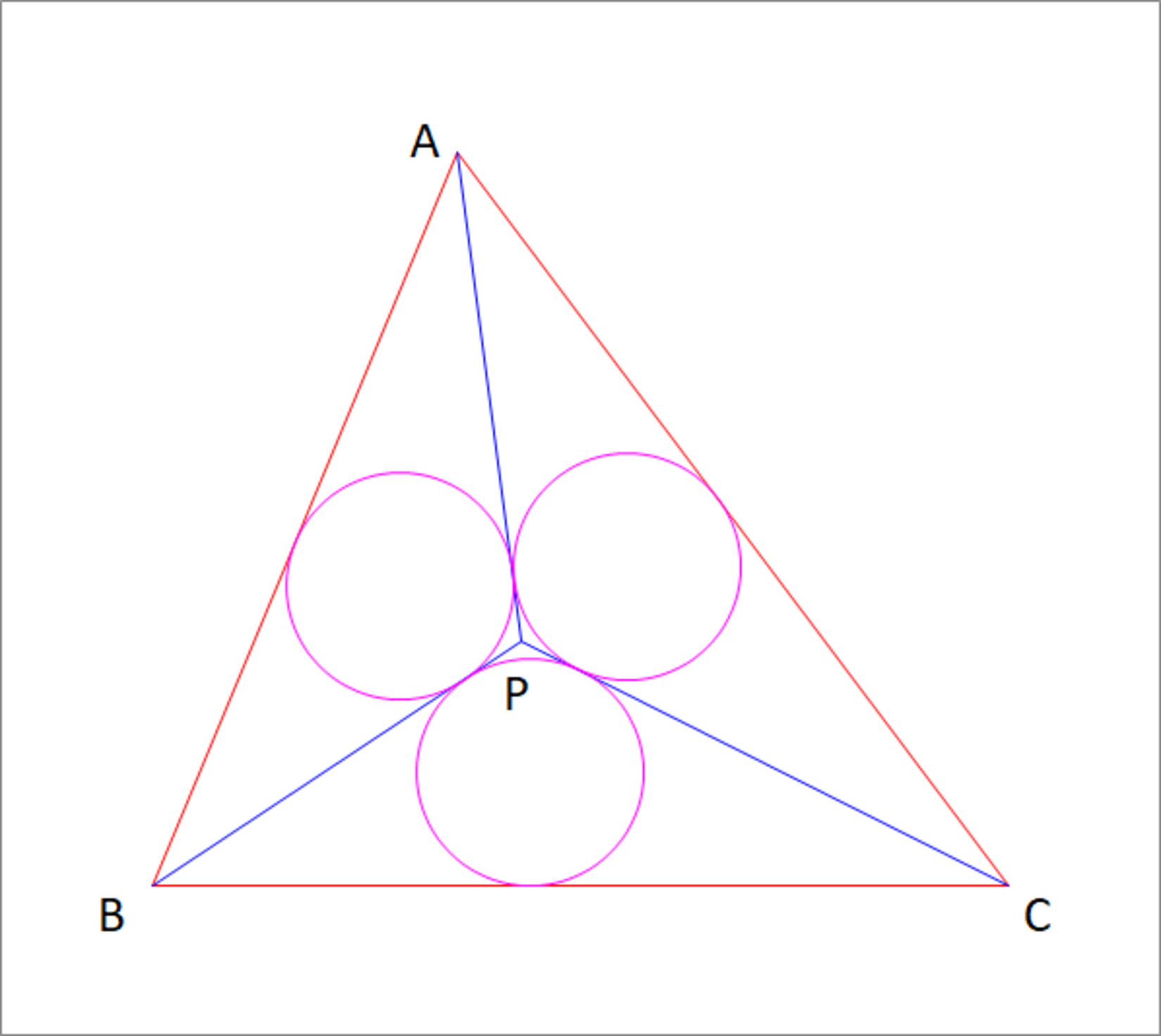
△ A B C has A B = 1 3 , B C = 1 4 , C A = 1 5 , you select a point P inside it, and connect P A , P B , P C , thus creating three triangles. If the incircles of △ A B P , △ A C P , △ B C P are identical, what is the radius r of each one of them? Enter ⌊ 1 0 5 r ⌋
The answer is 185754.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
P is the Congruent Incircles Point and is listed in as X 5 3 9 4 in Kimberling's Encyclopedia of Triangle Centers . Interestingly, no coordinates are known for point. However, Kimberling does offer an eight degree polynomial for finding the congruent inradius, as well as Mathematica code. The polynomial yielded an incorrect answer for me, but that was probably a careless transcription error on my part. So I resorted to numerical methods. I hope someone finds a more aesthetic solution.
Mine, posted at the same time as yours, is the same, except somehow less aesthetic!
Wow! Thanks, Chris.
What numerical methods did you use? I messed around with various approaches before diving in with coordinate geometry; for instance, setting up equations using the areas of the three triangles using Heron's formula and Δ = r s . The main stumbling block I had was that P A , P B and P C are not independent; but I don't know a (simple) way to relate them.
The fact ETC has no formula is definitely off-putting, but I wonder if careful choice of the equations to solve could at least lead to a nicer numerical method than I had.
Log in to reply
On the topic of congruent incircles, did you see this ? Eight equations, eight unknowns. This may just be the nature of the beast. Your solution may be the best we can do.
What interests me at the moment is how to find homogenous coordinates of a triangle center in terms of the triangle's sides and angles? I'm pretty naive about this, but I'm curious how folks discovered all those coordinates in ETC. And why they couldn't do it for the Congruent Incircles Point. Does the triangle center have to be geometrically constructable?
I used coordinate geometry. scipy.optimize does the heavy lifting. I wrapped it with a homegrown geometry library. Given P ( x , y ) it computes the three inradii and minimizes the range of [ r 1 , r 2 , r 3 ] tending to equality.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
|
1 |
|
I used coordinate geometry here; it's a bit messy but I'll outline the approach and some other findings.
The vertices of this particular triangle can be written as A ( 5 , 1 2 ) , B ( 0 , 0 ) , C ( 1 4 , 0 ) . Let P have coordinates ( x , y ) .
Since the area of any triangle is the product of its inradius with its semiperimeter, we have 2 [ Δ A P B ] = r ( A P + B P + A B ) and similarly for the other triangles. We can calculate the areas in terms of x and y using the shoelace theorem: 2 [ Δ B P C ] = 1 4 y 2 [ Δ C P A ] = 1 6 8 − 1 2 x − 9 y 2 [ Δ A P B ] = 1 2 x − 5 y
and the sidelengths involving P by Pythagoras: A P = ( x − 5 ) 2 + ( 1 2 − y ) 2 B P = x 2 + y 2 C P = ( 1 4 − x ) 2 + y 2
Putting all these together, we have x 2 + y 2 + ( 1 4 − x ) 2 + y 2 + 1 4 1 4 y = ( 1 4 − x ) 2 + y 2 + ( x − 5 ) 2 + ( 1 2 − y ) 2 + 1 5 1 6 8 − 1 2 x − 9 y = ( x − 5 ) 2 + ( 1 2 − y ) 2 + x 2 + y 2 + 1 3 1 2 x − 5 y = r
This can be solved numerically to give r = 1 . 8 5 7 5 4 … and an answer to the question of 1 8 5 7 5 4 .
With a bit of hunting on the Encyclopedia of Triangle Centres, this turns out to be centre X ( 5 3 9 4 ) , the "congruent incircles point". According to the ETC, r is the smallest positive root of this equation: 5 8 5 x 8 − 7 0 4 4 x 7 − 2 4 3 7 5 2 x 6 + 6 2 0 3 4 0 8 x 5 − 5 6 9 5 7 2 1 6 x 4 + 2 6 1 2 1 3 1 2 0 x 3 − 6 3 8 8 2 2 0 1 6 x 2 + 7 9 6 5 9 4 1 7 6 x − 3 9 8 2 9 7 0 8 8 = 0
I'd be interested in a proof of that one!