House Number

Firstly, it can not be a number between 50 and 59. The multiples of three between 50 and 59 are 51, 54, and 57. None of these numbers are multiples of 4, which means they would violate the second rule. This means the answer is not divisible by 3.

The rules for being between 60 and 69 include being divisible by 6 but not by 3. No number will ever satisfy this, so they're all out.

All that's left is to look at 70-79 for a number not divisible by 3 but is divisible by 4, and the only number to satisfy this is 76.

Here we have cases :

Case 1 (50-59) : Multiple of 3, multiple of 4, Multiple of 6... => No such number

Case 2(60-69): Not Multiple of 4, Not multiple of 3, Multiple of 6 => No such number

Case 3(70-79): Not multiple of 6, Not multiple of 3, Multiple of 4 => (Eureka) 76

Nailed it..!!!! Thats the number ;) ;)

I'm giving a logical reasoning as a solution of this one.. Clearly multiple of 6 AND 4 automatically turns out to be multiple of 3.. If we select any multiple of 3 in [50,59],we don't have any multiple of 4 or 6,which gives trouble according to the question. Next if we select any integer in [60,69] which is not a multiple of 4,we can't find any integer which is not a multiple of 3 but divisible by 6(its obvious!!). Next if we select any integer less than 50 or greater than 79,we might not find any of them which obeys the conditions correctly for obvious reason..!! So the required number must lie in [70,79] & must be a multiple of 4 but not a multiple of 6(ofcourse then its not a multiple of 3 also)!! Then it must be 76.. :-) :-)

Looks crazy but isn't To help your brain just write those numbers on a paper, Then look at the numbers between 50 and 59 , 51, 54 and 57 none of these are divisible by 2 meaning they aren't divisible by 4.

Then comes the second range, since 6=3x2 no number is divisible by 6 in that range , Narrowing all possibilities comes the third range.

We look for a number divisible by 4 and not by 3 which is 76.

First of all, think of a number that's NOT between 50-79. The rules for this number are

1. NOT a multiple of 3

2. A multiple of 4

3. A multiple of 6

Now, it's impossible for a multiple of 6 to not be a multiple of 3 so the number has to be between 50-79. Luckily, depending on the range, we can change 1 rule to it's inverse. And we have to change either 1 or 3, as those two conflict.

If we change rule 1, we need a multiple of 3,4, and 6 within 50 and 59. The lcm of these three numbers is 12, and no multiple of 12 is between 50 and 59.

If we change rule 3, we need a multiple of 4 but not of 3 or 6, or a multiple of 4 but not 3. The only multiples of 4 in this range are 72 and 76. 72 is divisible by 3, but 76 is not, so it is the solution.

Question is sometimes a bit confusing and that's because you cannot form any equations in this question to reach correct answer

It may appear tricky, although you''ll understand after solving that actually it isn't.

I tried this problem a couple of times, but did not get anything. So decided to write all numbers between 50 and 79 and got the answer 76. That consumed my 5-6 minutes.

Not a good way to approach. The solutions below are quite time saving.

I appreciate asker as well as all solution writers.

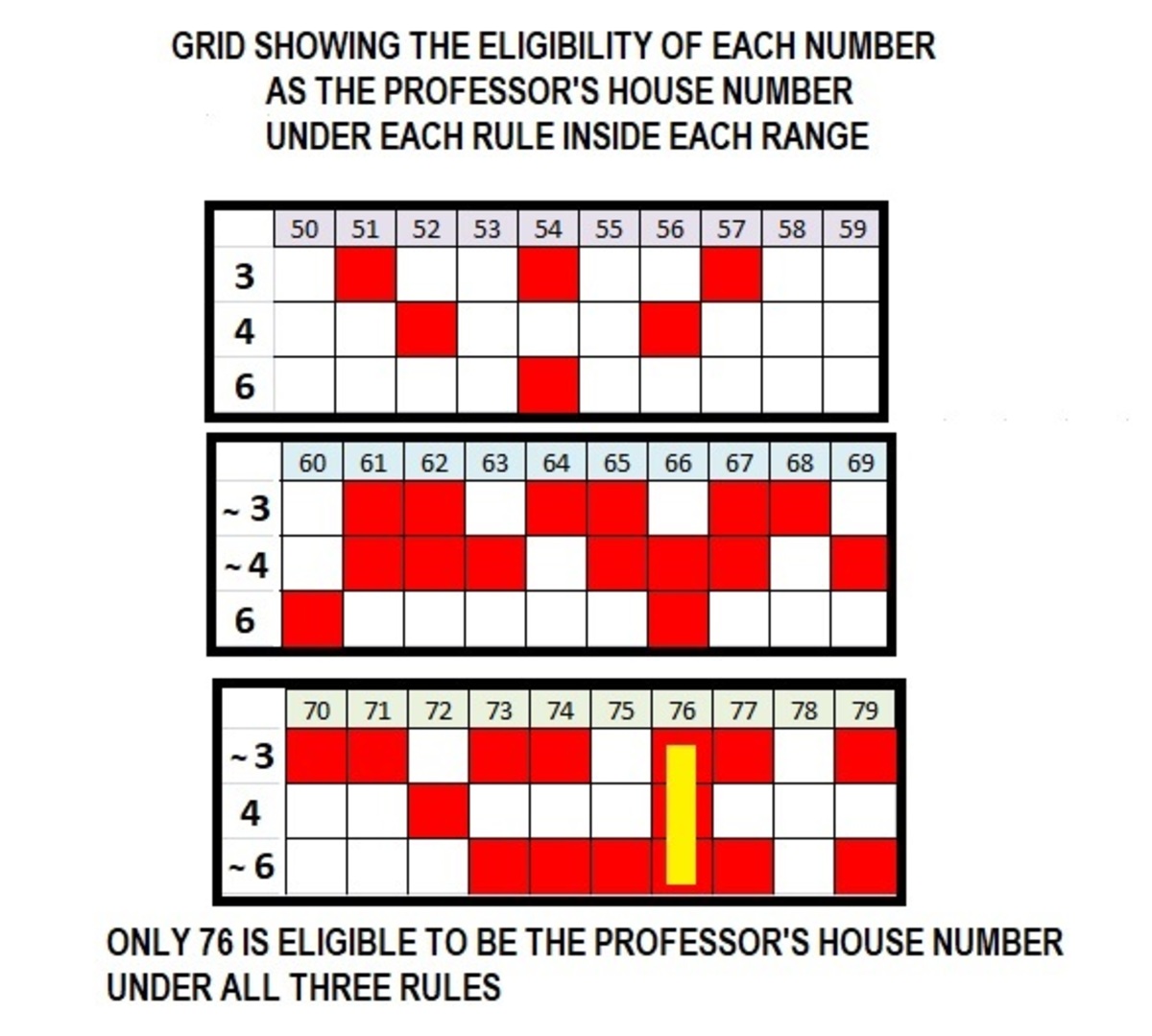76 is

not a multiple of 3 and thus is not required to be in 50-59.

is a multiple of 4 and thus is not required to be in 60-69. (not not a multiple of 4)

is not a multiple of 6 but is in the required range of 70-79.

All other number in the range 50-79 fail.

First guess... Simple process of elimination works well here

If the number is a multiple of 6, then (1) ensures that it is 54. But 54 does not satisfy (2).

Therefore, the number is not a multiple of 6, and (3) says that it is number from 70 to 79,

By (2), it must be a multiple of 4, hence either 72 or 76. But 72 violates (1).

Therefore the house number is 76.