House of Cards
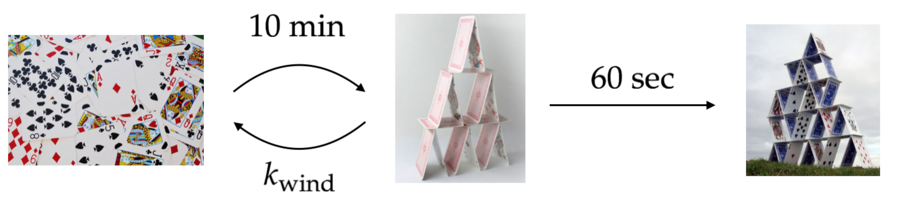 Suppose you're building a house of cards in your garage. At the beginning, you have a messy pile of cards lying on the ground. It takes you a long time to get the basic structure going (a three level house of cards). Once you have the basic structure, you can finish the house very quickly (gluing the cards together, to fix the structure permanently). However, the glue is very toxic, so you have to fix the structure outside. During this time, the assembled house of cards is susceptible to an intermittent wind, that can knock it down entirely.
Suppose you're building a house of cards in your garage. At the beginning, you have a messy pile of cards lying on the ground. It takes you a long time to get the basic structure going (a three level house of cards). Once you have the basic structure, you can finish the house very quickly (gluing the cards together, to fix the structure permanently). However, the glue is very toxic, so you have to fix the structure outside. During this time, the assembled house of cards is susceptible to an intermittent wind, that can knock it down entirely.
How long on average does it take you to finish the house of cards (in hours)?
Assumptions and Details
- It takes exactly 10 minutes to build the basic structure.
- Once the house of cards is built, it takes sixty seconds to reinforce with glue.
- Once the house of cards is standing, a wind comes by at random an average of once every twenty seconds ( s ).
- If the wind comes before the house is completely reinforced, the house will collapse.
The answer is 3.4583.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To solve this problem, we have to consider the sources of time.
One is the total amount of time spent stacking the house of cards., which is given by N h.o.c. × t h.o.c. , where t h.o.c. is equal to the time it takes to build the house, and N h.o.c. is equal to the expected number of times we need to repeat this act (due to the wind).
The second source is the average amount of time spent gluing the house which is given by t ˉ glue . Each time we get knocked down by the wind, we have to start over, building the house of cards, and then performing some fraction of the glue job before the wind comes and knocks it down again. Thus, the bar over t , indicating that we're taking the mean time. The partial glue job happens a total of ( N h.o.c. − 1 ) times (the last time takes the full t glue seconds).
The last source is amount of time we spend building and reinforcing in the last attempt, the time where everything works out. Thus, we have two numbers to calculate, N h.o.c. and t ˉ glue .
The indoor component of the house of cards construction is risk-free, it takes the same amount of time, every time, and always finishes. Thus, the variability comes in from racing the wind. Despite the wind coming an average of once every twenty seconds, we can find a window of sixty wind-free seconds if we're willing to wait long enough. How likely is this?
Consider an ensemble of infinitely many pre-build house of cards, all being glued outdoors in infinitely many separate windy environments. Now, let p + ( t ) be the portion of the structures which are not blown over by wind at time t . As any given system as the chance k wind d t of being knocked over per unit time, we expect the number of surviving systems to disappear like
p + ˙ ( t ) = − k wind × p + ( t )
which leads to p + ( t ) = exp − k wind t .
Thus, the chance for any given house to be standing after time t in the wind is given by p + ( t ) . Likewise, the expected number of times we will fail before successfully gluing the house in the wind is given by 1 / p + ( t ) .
Thus, we have N h.o.c. = p + − 1 ( 6 0 sec ) ≈ 2 0 . 0 9 .
As for t ˉ glue , we can once more exploit the distribution p + ( t ) to calculate the conditional average time for cases when the house of cards is blown over by wind, i.e. when t < 6 0 . This is given by
t ˉ glue = 0 ∫ t glue p + ( t ) d t 0 ∫ t glue t p + ( t ) d t
which is given by
t ˉ glue = k wind − 1 − e k wind t glue − 1 t glue ≈ 1 6 . 8 5 s
The total time taken is then
t total = N h.o.c. t h.o.c. + ( N h.o.c. − 1 ) t ˉ glue + t glue = e k wind t glue ( k wind − 1 + t h.o.c. ) − k wind − 1 ≈ 3 . 4 5 hr