How acute is your vision?
Geometry
Level
3
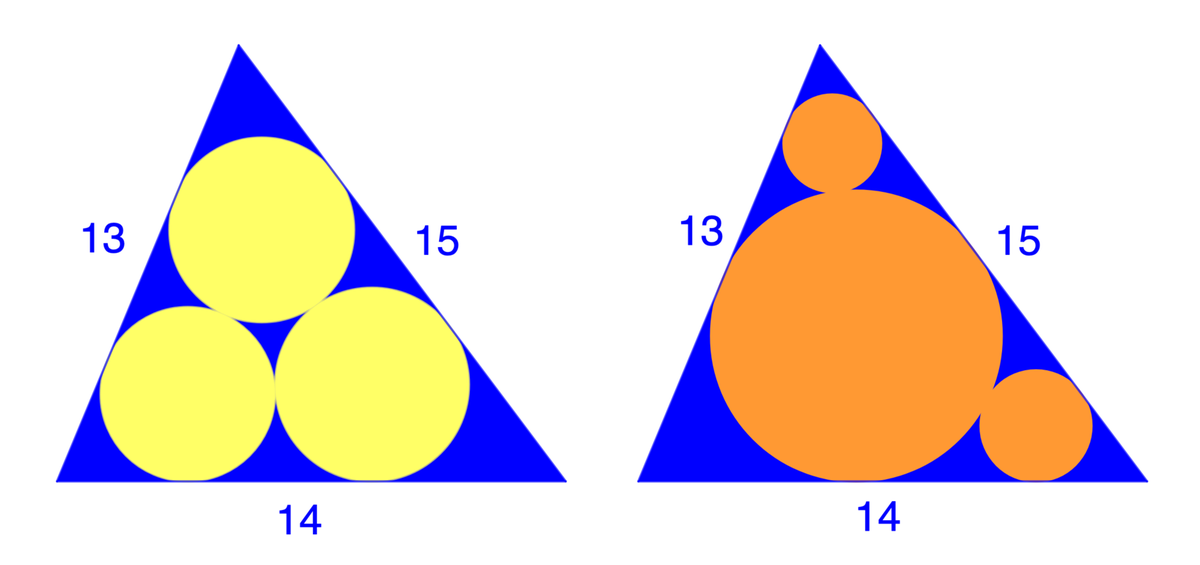
As shown above, three circles are inscribed in a triangle of side lengths 13-14-15 in two different ways. Which of these colored regions has a larger total area?
Yellow
Orange
They are both equal
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Notice that the largest orange circle is the triangle's incircle. This is all one needs know to answer this question. For three circles to provide maximum coverage of any triangle, a "greedy algorithm" must be used in constructing the circles, and this is what I used to create the triangle on the right. The largest possible circle is obviously the incircle, the other two orange circles are the largest which can be constructed in the remaining space. Thus, for the given triangle, the orange circles provide the maximum possible coverage. I wasn't up to typesetting the math to show this, but the bottom line is: orange = 63.3 and yellow = 60.8. Orange wins.
Interesting trivia: While it had been long been conjectured that a greedy algorithm was required, it wasn't proven until 1994. There is a nice discussion of this on Wikipedia's Malfatti Circles page.