How am I supposed to do that?
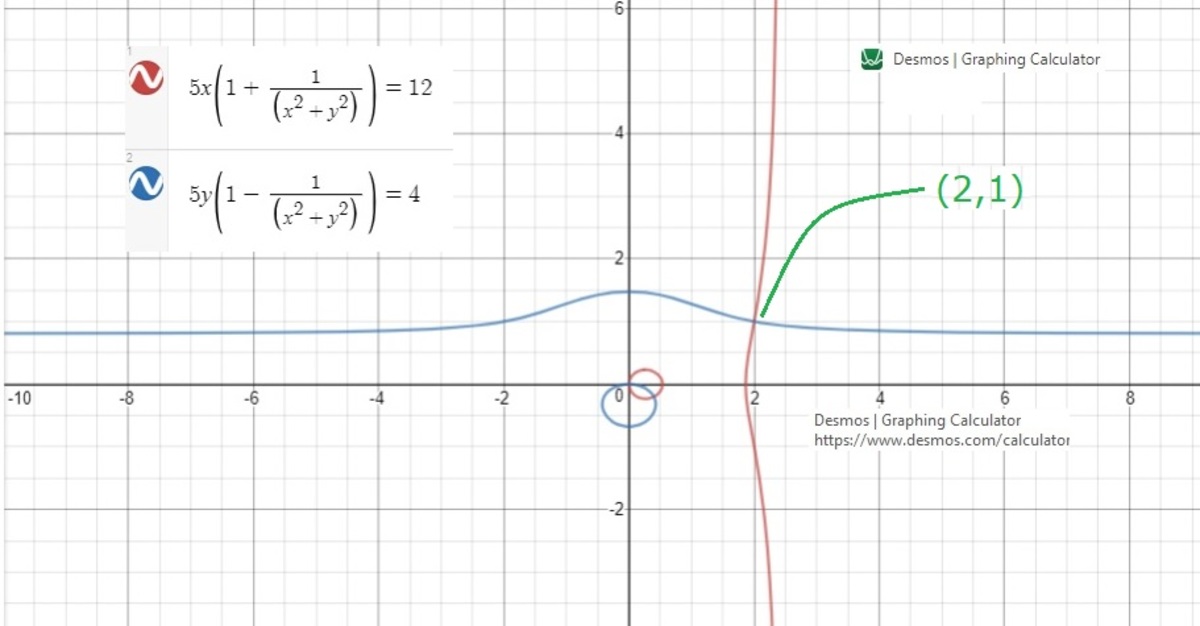
Solve the following system for real x and y 5 x ( 1 + x 2 + y 2 1 ) = 1 2 5 y ( 1 − x 2 + y 2 1 ) = 4
Note
- Enter your answer as the sum of all such values of x and y .
- This question once appeared in RMO.
The answer is 3.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Small typo. You interchange between m and t in the middle of your proof.
 ![]
![]
Let x 2 + y 2 = t > 0 . From the second equation, we can see that t = 1 . Also, the brackets in both equations must be non-zero, so we can write t = ( 5 ( t + 1 ) 1 2 t ) 2 + ( 5 ( t − 1 ) 4 t ) 2 1 6 2 5 = t 2 + 2 t + 1 9 t + t 2 − 2 t + 1 t = ( t + 1 ) 2 ( t − 1 ) 2 t ( 1 0 t 2 − 1 6 t + 1 0 ) 2 5 ( t 2 − 1 ) 2 = 1 6 0 t ( t 2 − 5 8 t + 1 )
P ( t ) = 2 5 t 4 − 1 6 0 t 3 + 2 0 6 t 2 − 1 6 0 t + 2 5 = 0
Nasty equation added to inventory! It's time to try guessing roots. The obvious − 1 , 0 , 1 give no decent results. Therefore, let's try rational roots.
We know that if b a is a root (with a , b coprime), then after multiplying P ( t ) by b 4 and taking the whole equation modulo a , we get 2 5 b 4 ≡ 0 . But a , b are coprime, so it implies a ∣ 2 5 . Similarly, we could take the whole equation b 4 P ( t ) = 0 modulo b , obtaining b ∣ 2 5 .
We're free to try roots b a = 2 5 1 , 5 1 , 5 , 2 5 (we've already tried 1 ). And, we can see that both 5 and 5 1 are roots. Factorising them out gives P ( t ) = ( t − 5 ) ( t − 5 1 ) ( 2 5 t 2 + 2 5 − 3 0 t ) = 0 and we can find out that 2 5 t 2 + 2 5 − 3 0 t = 0 has no real roots (its determinant is negative), so t must be either 5 or 5 1 .
The rest is trivial: plug both values of t = x 2 + y 2 into both initial equations and find the values of x , y .
1) 1 + 1/ (x^2 + y^2) = 12/ (5 x)
2) 1 - 1/ (x^2 + y^2) = 4/ (5 y)
2 = 4/ 5 (3/ x + 1/ y)
y = 2 x/ (5 x - 6)
Since x <>0,
125 x^4 - 600 x^3 + 1045 x^2 - 780 x + 180 = 0
Divides with G.C.D. of 5 to polynomial equation obtained:
25 x^4 - 120 x^3 + 209 x^2 - 156 x + 36 = 0 {Ignore "How I am suppose to do that?"}
x1 = 1.2 - j 0.6
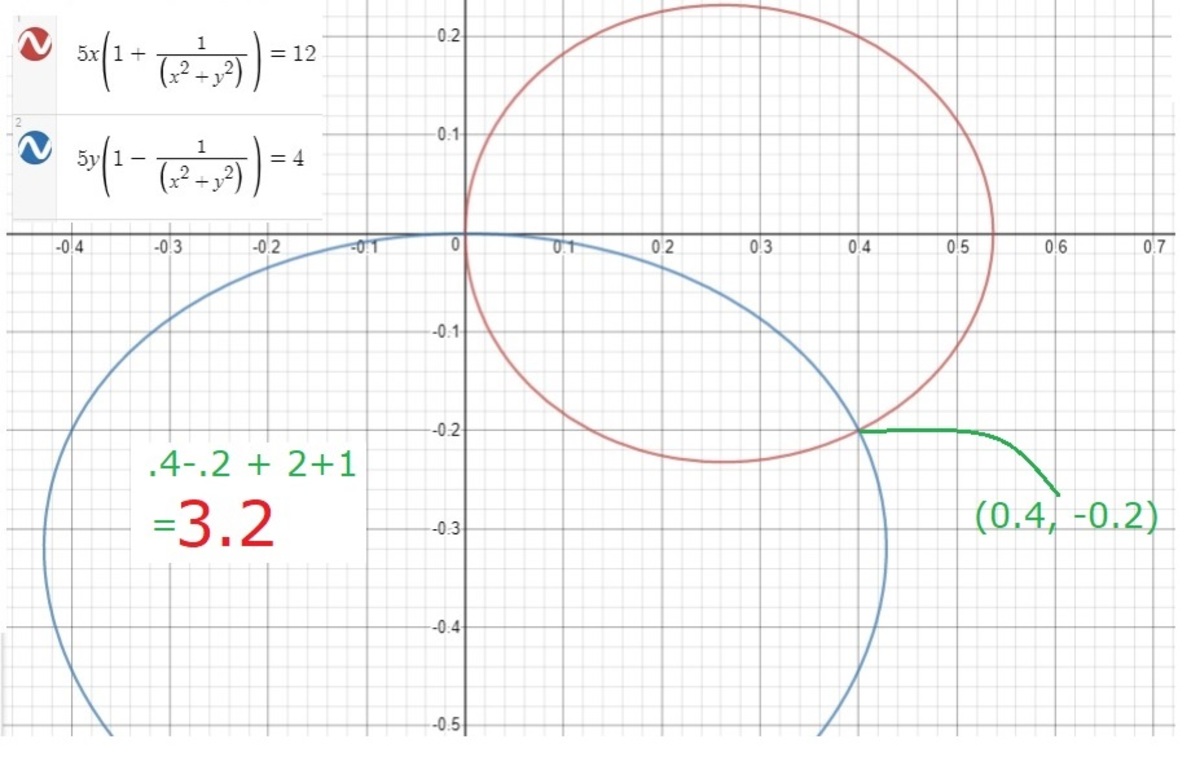
x2 = 0.4
x3 = 2
x4 = 1.2 + j 0.6
Substitute real x to check with y for original equations:
x = 0.4; 2 sum = 3.2
y = -0.2; 1
Eq1 = 12; 12
Eq2 = 4; 4
Answer: 3.2
Let z = x + i y where i = − 1 .Then x 2 + y 2 = z ( x − i y )
x + x 2 + y 2 x = 5 1 2 ...(1)
y − x 2 + y 2 y = 5 4 .....(2)
( 1 ) + i × ( 2 ) gives
x + i y + x 2 + y 2 x − i y = 5 4 ( 3 + i )
or, z + z 1 = 2 t where t = 5 2 ( 3 + i )
Solving , z = t + t 2 − 1 or z = t − t 2 − 1
t 2 − 1 = 2 5 1 ( 5 + 2 4 i ) = ( 5 4 + 3 i ) 2
So , z = 5 6 + 2 i + 5 4 + 3 i or z = 5 6 + 2 i − 5 4 + 3 i
Comparing, x = 2 , y = 1 or x = 5 2 , y = − 5 1