How big is the orange?
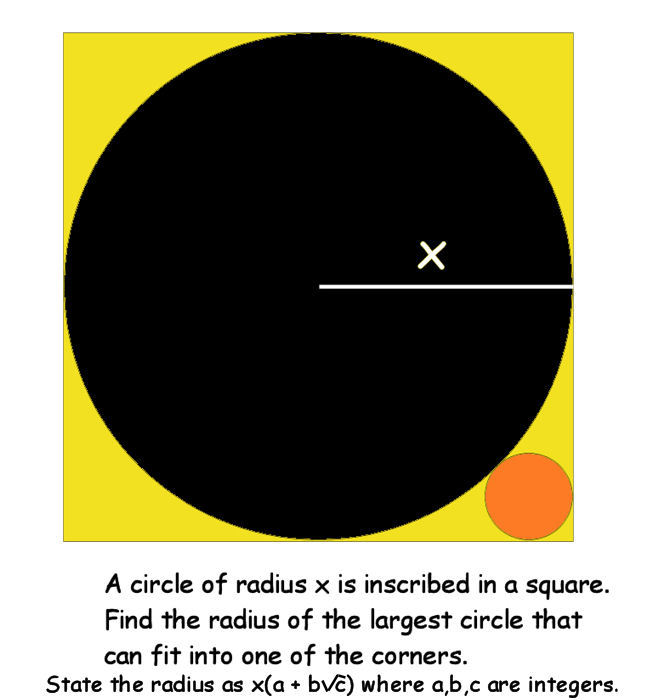A circle of radius x is inscribed in a square. What is the radius
r
of the largest circle that can fit into one of the corners?
State the radius as r = x ( a + b c ) where a , b , c , are integers and c is not divisible by the square of any prime. Find a + b + c .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
title
<br>a+b+c= 3+(-2)+2 = 3
I'm disappointed that there weren't more attempts at this problem. Its solution is comparatively easy. I was leading up to a similar case but in 3 dimensions which would really challenge you.
Log in to reply
Have you posted the 3-dimensions case? If so, you should link it.
Looking 4wrd to d 3D problem.By the way how about generalizing this problem for the nth corner circle.Can it be done?
I did the same way..
a = 3 , b = − 1 , c = 8 is also a valid answer, so maybe you should specify b , c as coprime.
Equating the 2 formulas for half of the diagonal of the square: x 2 + x 2 x 2 x ( 2 − 1 ) r r r r r = x + r + r 2 + r 2 = x + r + r 2 = r ( 1 + 2 ) = x ( 2 + 1 ) ( 2 − 1 ) = x ( 2 + 1 ) ( 2 − 1 ) ( 2 − 1 ) ( 2 − 1 ) = x 2 − 1 2 − 2 2 + 1 = x ( 3 − 2 2 ) = x ( a + b c ) , a = 3 , b = − 2 , c = 2
Thus, a + b + c = 3 − 2 + 2 = 3
completely wrong concept
Log in to reply
Can you elaborate, in what sense is this a "completely wrong concept"?