This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let A be left top corner of small square ABCD, side S, go counter clockwise, O the center to the right.
M midpoint of AB, N of DC.
2
∗
N
O
=
s
i
d
e
o
f
t
h
e
b
i
g
s
q
u
a
r
e
=
2
.
∵
c
i
r
c
l
e
D
i
a
m
e
t
e
r
=
B
i
g
s
q
u
a
r
e
D
i
a
g
o
n
a
l
.
I
n
r
t
.
Δ
A
M
O
:
−
M
O
=
S
+
N
O
=
S
+
2
2
.
A
M
=
2
1
∗
S
H
y
p
.
A
O
=
1
.
∴
M
O
2
+
A
M
2
=
A
O
2
,
⟹
(
S
+
2
2
)
2
+
(
2
1
∗
S
)
2
=
1
.
S
o
l
v
i
n
g
q
u
a
d
r
a
t
i
c
i
n
S
,
4
5
∗
S
2
+
2
∗
S
−
2
1
=
0
,
S
2
=
2
5
2
=
0
.
0
8
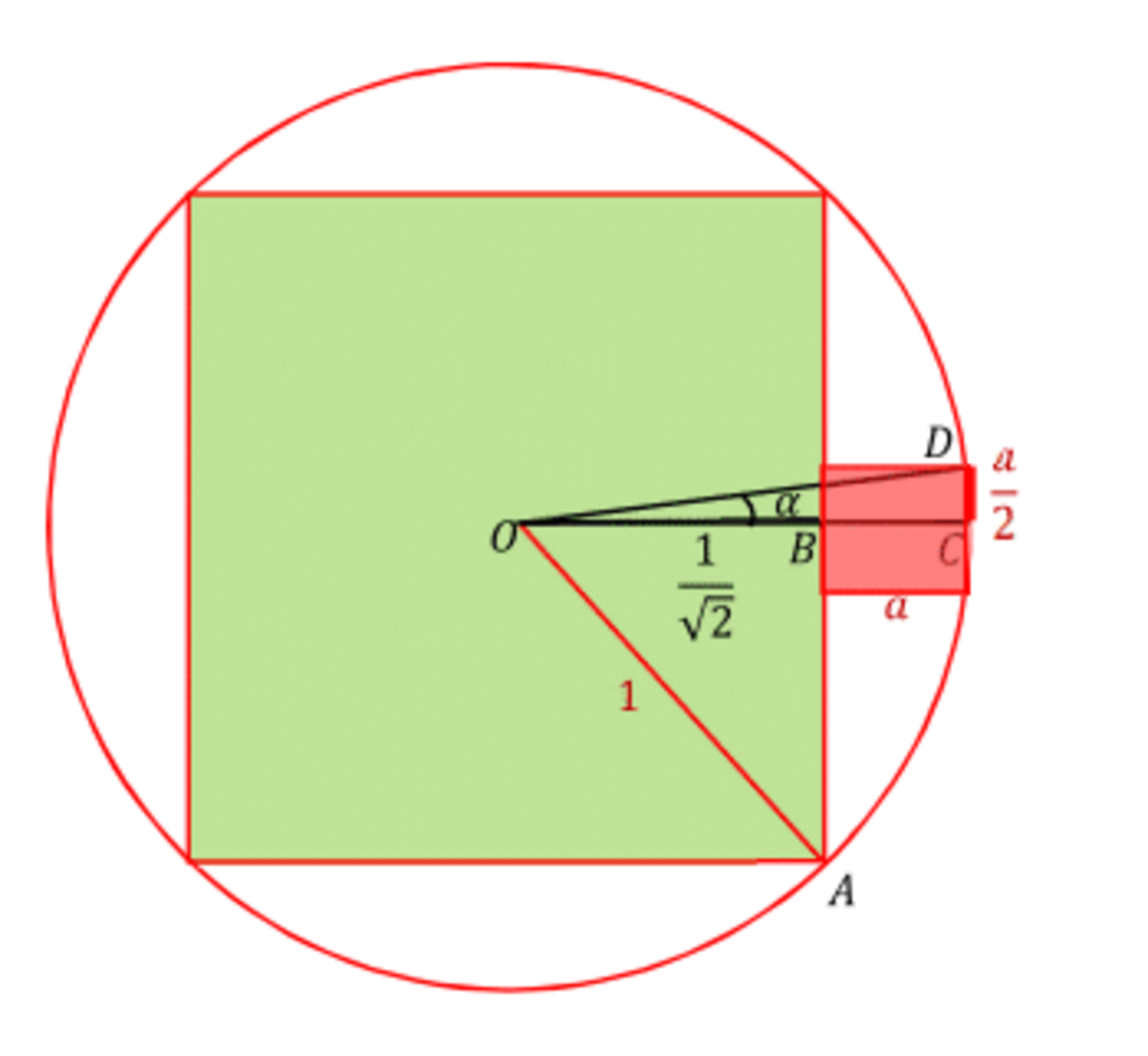 Side of red square,
a
, is the difference between
O
C
=
cos
α
and
O
B
=
2
1
.
Side of red square,
a
, is the difference between
O
C
=
cos
α
and
O
B
=
2
1
.
a = cos α − 2 1
From △ D C C we can see that 2 a = sin α or a = 2 sin α
Comparing the two produces an equation in sin α
1 − sin 2 α − 2 1 = 2 sin α
the solution of which is sin α = 2 5 1
From that a = 2 sin α = 5 2
and the area A = a 2 = 2 5 2 = 0 . 0 8
Suppose the unit circle is centered at the origin and the red square is symmetric about the (negative) x -axis.
A diagonal of the green square has the same measure as the diameter of the circle, so the side of the square has length 2 2 = 2 . The leftmost side of the green square thus lies along the line x = − 2 2 .
Now the equation of the unit circle is x 2 + y 2 = 1 . So if the y -coordinates of the upper and lower vertices of the red square are a and − a , respectively, (with a > 0 ), then the height of the red square will be 2 a and the width will be 1 − a 2 − 2 2 . Since the height and width must be equal, we must have
1 − a 2 − 2 2 = 2 a
⟹ ( 1 − a 2 ) − 2 ( 1 − a 2 ) + 2 1 = 4 a 2
⟹ − 2 ( 1 − a 2 ) = 5 a 2 − 2 3
⟹ 2 − 2 a 2 = 2 5 a 4 − 1 5 a 2 + 4 9
⟹ 1 0 0 a 4 − 5 2 a 2 + 1 = 0
⟹ a 2 = 2 0 0 5 2 ± 5 2 2 − 4 ∗ 1 0 0 = 2 0 0 5 2 ± 4 8 ,
so either a 2 = 2 1 or a 2 = 2 0 0 4 = 5 0 1 . Now the first of these corresponds to the green square, so for the red square we must have that a 2 = 5 0 1 .
The area of the red square will then be ( 2 a ) 2 = 4 a 2 = 5 0 4 = 2 5 2 = 0 . 0 8 .