How can you relate these two points?

Geometry Level 5

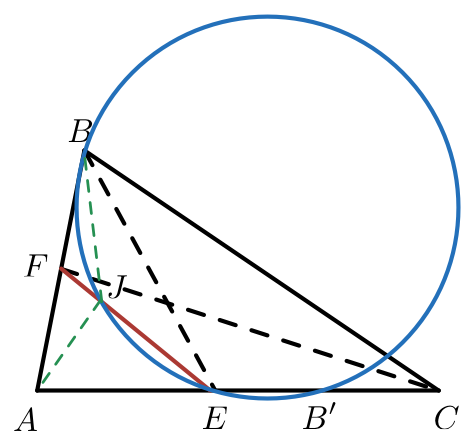In $\triangle ABC$ , $\angle A=80^\circ, \angle B=65^\circ ,\angle C=35^\circ$ . The internal angle bisectors of $\angle B,\angle C$ meet their respective opposite sides at $E,F$ . Let $B'$ be a point on segment $AC$ such that $AB'=AB$ . Let the circumcircle of $BB'E$ intersects $FE$ at $J$ .

Find the measure (in degrees) of $\angle AJB$ .

The answer is 165.

2 solutions

Xuming Liang
Aug 10, 2015

We extend $FE$ to meet $BC$ at $K$ . It is a well known fact that $AK$ is external angle bisector of $\angle A$ . Note that $\angle BJF=\angle BB'A=90-\frac {\angle A}{2}=\angle BAK$ , this means $B,J,A,K$ are concyclic $\implies \angle AJB=180-\angle AKB=180-(\angle B-90+\frac {\angle A}{2})=\boxed {165}$ .

To prove the well known property mentioned above, it suffices to show tht $\frac {KB}{KC}=\frac {AB}{AC}$ , which can be done using Menelaus's theorem.

Hadia Qadir
Aug 18, 2015

I began by redrawing the diagram. Extending a couple of lines suggested themselves, and it is found that a simple proof can be made to show that angle AJB = 165 degrees.

How can you relate these two points?

The answer is 165.

2 solutions

0 pending reports