How do I fire?

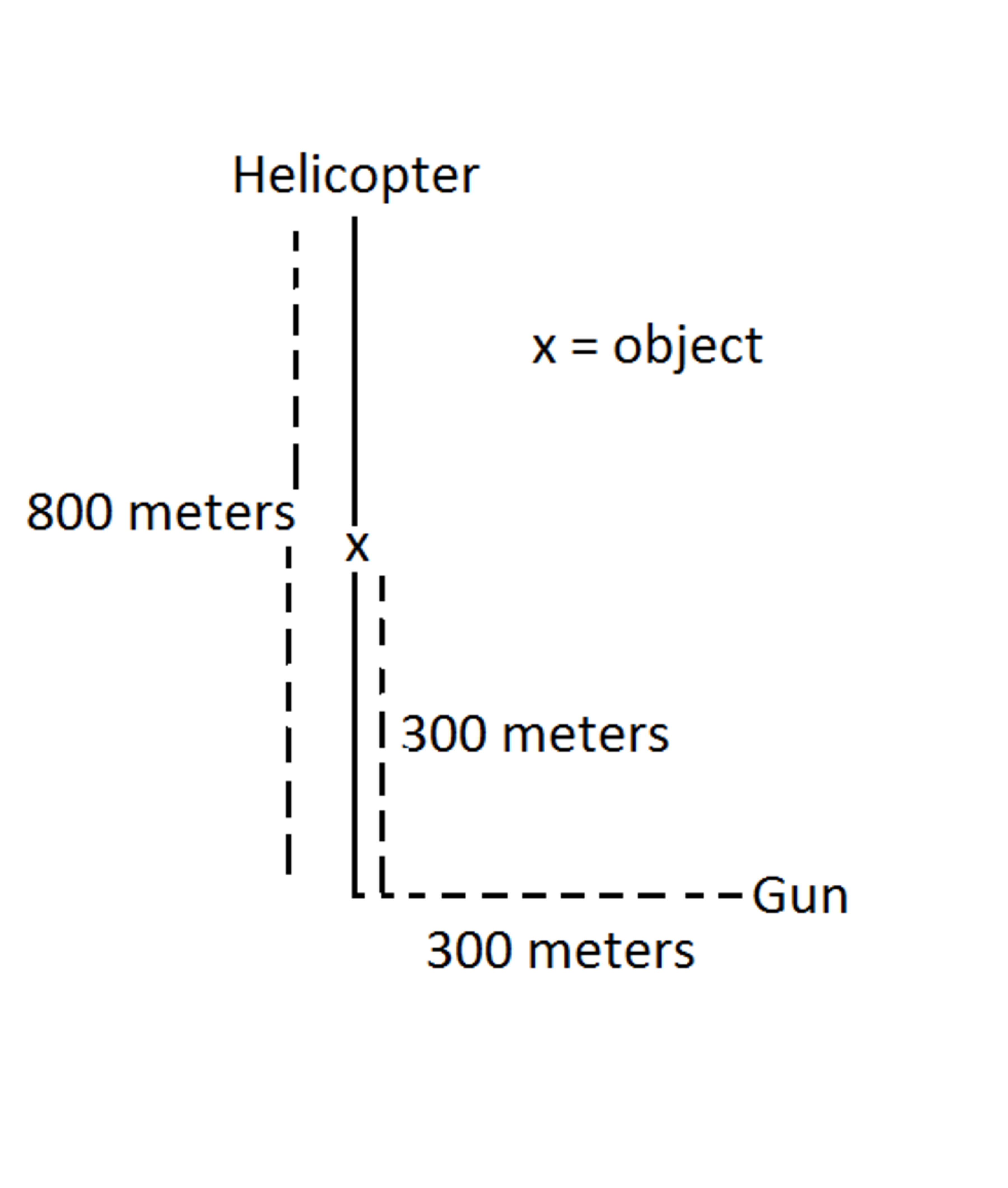
Classical Mechanics Level pending

For firing practice,an object is dropped from a helicopter 800 meters above the ground. A gun is horizontally 300 Meters away from the helicopter and has a firing speed of 150 meters/second. The object must be hit at a height of 300 meters above the ground. To the nearest degree, at what angle to the horizontal must the gun be fired?

48° 49° None of the rest 47° 46°

2 solutions

Aamir Faraaz
Jan 20, 2016

Shouldn't it be 45 degrees Siam?

Syed Baqir
Sep 6, 2015

$Speed\quad =\quad \begin{cases} 150\quad cos\theta \\ 150\quad sin\theta \quad -\quad gt \end{cases}$

$\because \quad Distance=\quad \begin{cases} 150\quad (t)\quad cos\quad \theta \\ 150\quad (t)\quad sin\quad \theta \quad -\quad \frac { 1 }{ 2 } \quad (g)\quad ({ t) }^{ 2 } \end{cases}$

$\therefore \quad 300\quad =\quad 150\quad (t)\quad cos\theta$

$150\quad sin\theta \quad -\quad g(t)\quad 0\quad \Longleftrightarrow \quad 150\quad sin\theta \quad =\quad g(t)$

$\Longrightarrow \quad t\quad =\quad \frac { 150\quad sin\theta }{ g }$

Substitude :

$300\quad =\quad 150\quad (\frac { 150\quad sin\theta }{ g } )\quad cos\theta$

$2g\quad =\quad 75\quad *\quad 2\quad sin\theta \quad *\quad cos\theta$

$2g\quad =\quad 75\quad *\quad sin\quad (2\theta )$

$\Rrightarrow \theta \quad =\quad 7.58^{ 0 }$

How do I fire?

2 solutions

0 pending reports