How do the rectangles' areas compare?

${\color{#D61F06}\text{This problem's question:}}$ How do the rectangles' areas compare?

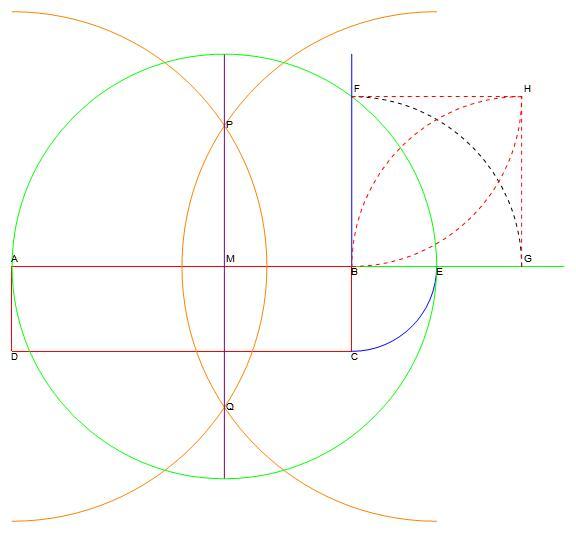
The construction:

1. ABCD is the given rectangle.
2. Extend AB (green in the illustration).
3. Make an arc centered on B from C to where it encounters the AB (green) line. Label the intersection E.
4. Construct a perpendicular bisector between A and E. This is the two orange arcs of the same but not specific radius, the points where the two arcs intersect labeled P and Q and then draw a straight line (purple in the illustration) between P and Q to intersect AE. Label that last intersection M.
5. Draw a circle (green in the illustration) of radius ME centered at M.
6. Extend side CB this line is blue in the intersection) to where it intersects the previous circle. Label this point F.
7. Draw a arc (dashed black in the illustration) of radius BF centered at B to where it intersects the AE extension. Label this point G.
8. Draw a arc (dashed red in the illustration) of radius BG centered at G to where it intersects the AE extension. Draw a arc (also dashed red in the illustration) of radius FB centered at F to where it intersects the previous arc. Label this point H.

The new rectangle is BFHG and by construction, it is square.