How do they do it?
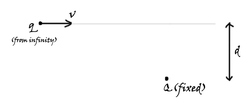 Let a charge
Q
be held fixed in space. Another charge
q
of mass
m
is thrown with a velocity of
v
from an infinitely far place, as shown in the figure, such that it is at a separation of
d
initially.
Let a charge
Q
be held fixed in space. Another charge
q
of mass
m
is thrown with a velocity of
v
from an infinitely far place, as shown in the figure, such that it is at a separation of
d
initially.
Find the minimum distance (in m ) between the two charges.
Details and Assumptions
∙
Q
=
5
μ
C
∙
q
=
1
μ
C
∙
d
=
3
cm
∙
v
=
2
m/sec
∙
m
=
1
g
The answer is 22.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Discussions for this problem are now closed
Can't we apply maxima minima concept in finding the minimum distance?
Sorry, but I don't understand why the minimum distance should be stationary? Actually, I don't understand the 'perpendicular velocity' part.
Using the same reasoning of Sinha, the minimum distance r between the two charges [Q] and [q] occurs when the line joining the two charges (shown vertical in the diagram) is perpendicular to the line of approach of [q] from infinity (shown horizontal). At this point the velocity of charge [q] is 0. All its kinetic energy is converted to potential energy. Equating the two energies, we have:
r 2 k e Q q ( r − d ) = 2 1 m v 2 , w h e r e k e i s C o u l o m b ′ s c o n s t a n t ( 8 . 9 8 7 6 × 1 0 9 N m 2 C − 2 . .
This can be resolved the quadratic equation below:
m v 2 r 2 − 2 k e Q q r + 2 k e Q q d = 0 .
Solving the equation gives r = 2 2 . 4 9 3 .
May be I did some thing wrong coz the square of my answer is 22.5009. I used conservation of angular momentum and mechanical energy
Okay I got it I put an extra square of didt. in potential energy How silly
Here in this question the minimum distance between charge q and Q will be when all the kinetic energy of charge q thrown from infinity gets converted to potential energy between q and Q.... and the charge q temporarily comes to rest ....!! By law of conservation of energy :- initial PE (between q and Q) + kinetic energy of q = final PE (between q and Q) + final kinetic energy of q 0 + 1/2 m v^2 = ( k * q *Q)/ r + 0
putting the values given:- m = 1g v = 2m/s q = 1micro coulomb Q = 5 micro coulomb take k (coulombs constatnt) = 9* 10^9 (N-M^2/C^2) unit r = let r be the nearest distance (m) ALL THE UNITS CONVERTED IN SI UNIT FORM....
1/2 * 1/1000 * 2^2 =[ ( 9* 10^9 ) * (1 10^-6 ) * ( 5 10^-6)]/ r
r = 45/2 = 22.5 m !!!!!!
Expanding the solution of @abdulmuttalib lokhandwala .
Note that at the point of closest approach, the velocity u of the particle with charge q should be at right angle to the line-segment joining the charge Q and q . Otherwise u would have a component in (or opposite to) the direction of charge Q and hence the distance would not be stationary. Using the above observation, we can write down an equation for conservation of angular momentum of the moving particle w.r.t. the stationary particle (conservation of angular momentum holds since the electrostatic force is radial)
m v d = m u d min , i.e. u = v d / d min
We also assume conservation of energy in this problem (the charge actually radiates some electromagnetic energy as it accelarates, but this effect is absolutely negligible at this scale of speed). This gives the equation
2 1 m v 2 = 2 1 m u 2 + 4 π ϵ 0 1 d min Q q
Substituting for u and re-arranging the above equation we obtain the following quadratic equation
x 2 − E K E P x − 1 = 0
Where x = d d min , E P = 4 π ϵ 0 1 d Q q , E K = 2 1 m v 2 . Solving the above equation we obtain d min = 2 2 . 5 m .