How Do You Relate These Points Now?
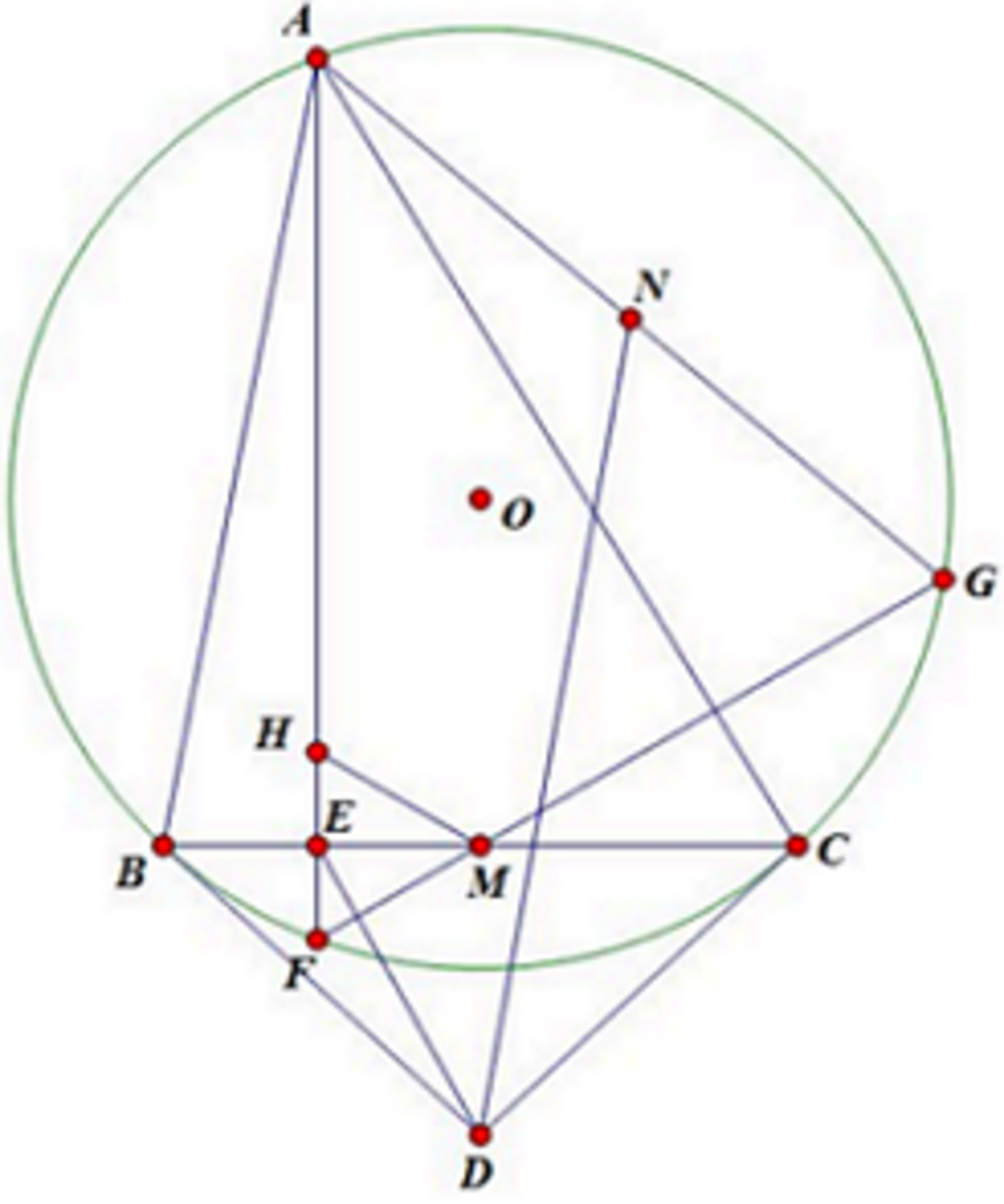
Let and denote the circumcenter and the orthocenter of respectively with midpoint of at .
The tangents at to meet at . Construct respectively. again at ; is the midpoint of .
Suppose . Find in degrees.
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We claim that ∠ E D N = ∠ M D G .
Connect G D which interesects ⊙ A B C at L , G . Since G M , G D are isogonals wrt ∠ B G C because G D is a symmedian of G B C , therefore A L , A F are isogonals wrt ∠ B A C , which means L ∈ A O and D G ⊥ A G . Moreover lines D F , D G are symmetric about D M .
We now show D G N O ∼ D M E F by individually proving G O N ∼ M F E , D G O ∼ D M F .
The first is trivial by property of circumcenter. For the second, we have ∠ O D G = ∠ F D M by symmetry mentioned above. Since O G = O L , thus ∠ O G D = ∠ O L G = ∠ A F D = ∠ D M F and the similarity is established.
From the similarity we have ∠ E D M = ∠ N D G ⟹ ∠ E D N = ∠ O D G , which is what we desired to show. By some angle chasing or the fact that O L 2 = O C 2 = O M ⋅ O D , we can obtain ∠ O D G = ∠ O L M . Hence:
∠ E D N + ∠ H M B = ∠ O L M + 9 0 − ∠ M H E = 9 0 − ( ∠ L H E − ∠ A L H ) = 9 0 − ∠ H A O = 9 0 − ∣ ∠ . B − ∠ C ∣ = 7 0