How does one raise one's self?
1 1 2 2 3 3 4 4 5 5 = = = = = 1 4 2 7 2 5 6 3 1 2 5
Victoria just started learning about exponentiation in class, and she has written down the 5 equations above. She then postulates that
x x is a strictly increasing function for positive x .
Is her claim correct?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice! A simpler way to solve this is to bring up a counterexample like ( 2 1 ) 2 1 = ( 4 1 ) 4 1 .
Log in to reply
You are much better than I.
Log in to reply
Haha! Thanks. You're pretty good yourself ;) ;) ;) ;) ;)
It really suffices to give a concrete counterexample . ( 4 1 ) 1 / 4 = 2 1 ; \ ( 2 1 ) 1 / 2 = 2 1 . Clearly, the function is not strictly increasing between x = 4 1 and x = 2 1 .
Calculus proof
To simplify work, I consider the (natural) logarithm, f ( x ) = ln x x = x ln x . Since the logarithm, defined on positive x , is a strictly increasing function, we can consider the behavior of f instead of x x .
Now f ′ ( x ) = 1 + ln x , so that the function f may have an extreme value if f ′ ( x ) = 0 ∴ x = e − 1 ≈ 0 . 3 7 .
Taking second derivatives, we find f ′ ′ ( x ) = x 1 > 0 , so that f is concave on the entire domain. This shows that f ′ ( x ) < 0 (and therefore x x is decreasing) for 0 < x < e − 1 .
Victoria's claim is incorrect.
BESTEST SOLUTION!
Isn't f a strictly convex (concave up) function?
Concavity (concave down) would require non-positive second derivative.
A doubly differentiable function f is strictly convex on an interval iff f ′ ′ ( x ) < 0 on that interval.
The simplest example is the convex parabola f ( x ) = − x 2 .
Log in to reply
Wikipedia and Wolfram|MathWorld say the exact opposite.
Here's what Chew-Seong Cheong is talking about, see his solution
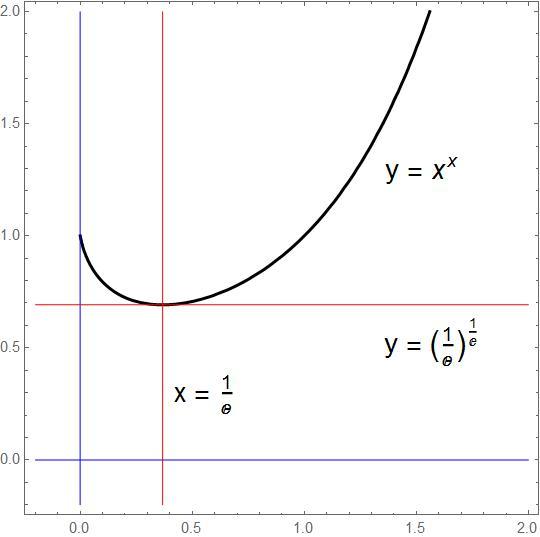
Let f ( x ) = x x for x > 0 . Then its first derivative f ′ ( x ) = ( ln x + 1 ) x x . Note that f ′ ( x ) < 0 , when x < e 1 . Therefore, x x is decreasing between 0 < x < e 1 and increasing when x > e 1 . No, she is not correct .