How Eg-No-Ra-Moose Can You Be?

Logic Level 3

Joe is playing a game involving the above board. He places 14 pegs on the board, leaving a single space empty. He then jumps a peg with an adjacent peg. The peg that has been jumped is removed.

For example, if Joe jumped the bottom-left yellow peg with the bottom-left red peg, then he would need to remove the yellow peg and move the red one to the space above the blue, on the third row.

The game ends when no more moves are possible.

What is the maximum amount of pegs that can be left when the game is over?

Note : I am not asking what the maximum possible number of pegs without any possible moves is--you must be able to get to the position by playing the game.

7 8 9 10 11 12

2 solutions

Alex Li
Aug 22, 2016

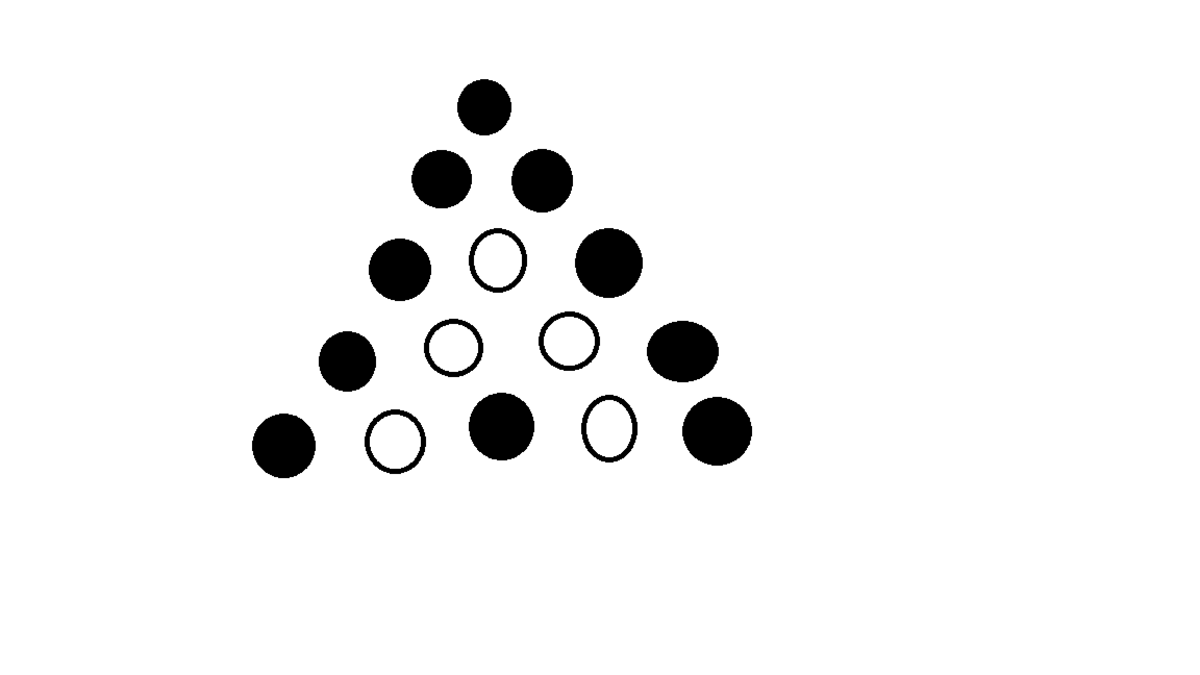
I don't really have any proof that this is the minimum, but informally, it seems to be that the only other 'losing' positions obtainable with more than 10 pins are the two below, and by working backwards, it's easy to see that you can't get to them without 3 and 2 starting holes, respectively. EDIT: Brute-force solution in python from a friend

https://repl.it/DN1h/1

import copy

directions = [(0, -1), (0, 1), (-1, 0), (1, 0), (-1, -1), (1, 1)]

def add(v1, v2):
    return (v1[0]+v2[0], v1[1]+v2[1])

def value(board):
    return sum(sum(board, []))

def getpiece(board, pos):
    if pos[0] >= 0 and pos[0] < 5 and pos[1] >= 0 and pos[1] < 5 and pos[0] >= pos[1]:
        return board[pos[0]][pos[1]]
    else:
        return 2

def neighbors(board):
    result = []
    for i in range(0, 5):
        for j in range(0, i+1):
            pos = (i, j)
            if getpiece(board, pos) == 1:
                for dir in directions:
                    if getpiece(board, add(pos, dir)) == 1 and getpiece(board, add(add(pos, dir), dir)) == 0:
                        neighbor = copy.deepcopy(board)
                        neighbor[i][j] = 0
                        neighbor[i+dir[0]][j+dir[1]] = 0
                        neighbor[i+2*dir[0]][j+2*dir[1]] = 1
                        result.append(neighbor)
    return result

def main():
    reachableBoards = [[[0], [1, 1], [1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1, 1]], [[1], [0, 1], [1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1, 1]], [[1], [1, 1], [0, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1, 1]], [[1], [1, 1], [1, 0, 1], [1, 1, 1, 1], [1, 1, 1, 1, 1]]]
    parentBoards = [[], [], [], []]
    boardsUnexplored = copy.deepcopy(reachableBoards)
    while boardsUnexplored:
        curBoard = boardsUnexplored.pop()
        for neighbor in neighbors(curBoard):
            if neighbor not in reachableBoards:
                reachableBoards.append(neighbor)
                parentBoards.append(curBoard)
                boardsUnexplored.append(neighbor)
    maxValue = max([value(b) if not neighbors(b) else 0 for b in reachableBoards])
    for b in reachableBoards:
        if value(b) == maxValue and not neighbors(b):
            curBoard = b
            print()
            while curBoard != []:
                print(curBoard)
                curBoard = parentBoards[reachableBoards.index(curBoard)]

main()

Label the spots with A, B, C such that no two adjacent spots have the same label. (There is only one way to do this, up to permutation of the labels.) Each letter will appear exactly 5 times. At the beginning, one of the spots is a hole, so there are 5 pegs of two of the letters and 4 pegs of the other letter; WLOG there are 5 A's, 5 B's, and 4 C's. Each move will change the number of pegs of each letter by exactly 1. Thus the parity difference will remain; C's will have a different parity from A's and B's. (If there are an even number of C pegs, then there will be an odd number of A pegs and an odd number of B pegs, and similarly if there are an odd number of C pegs.)

With that known, now we can easily rule out positions where the numbers of pegs of each label have the same parity, since it cannot be generated. For example, the triangle board at the end has 4 of each, which have the same parity, so it cannot be generated. Now just generate all $2^{15}$ possible positions, check that there is no legal move by computer (easy), check that the parities are not all same (also easy), and give the list of the remaining ones. Now you can try each of them from the one with the largest number of pegs remaining, trying to make a game that leads to that position. I'm not sure how you can determine whether it's possible without testing every possible play or something, but luckily apparently 10 pegs is achievable, and thus a computer can run it fairly quickly. (There are 36 possible moves that need to be checked each position, so a 10-peg position means 4 moves and thus $36^4$ games to check. And checking that no 11-peg position or more is possible can be done in $36^3$ moves per position, and while I haven't actually done the computation, there shouldn't be too many positions to check. Quick enough.)

(This is a comment and not a solution because my intuition didn't lead me to the 10-peg position; I only had a 8-peg position.)

Ivan Koswara - 4 years, 9 months ago

You might be interested in this webpage !

Mark Hennings - 4 years, 9 months ago

Once I was playing this and somehow managed to get just the perimeter left, thus ending the game.

Cohen Campbell - 2 years, 5 months ago

Justin Park
Apr 21, 2020

stable configuration with 12 exists, but unachievable in a game

stable configuration with 11 does not exist

stable configuration with 10 exists and is achievable

below is a roughly drawn final configuration.

How Eg-No-Ra-Moose Can You Be?

2 solutions

0 pending reports