How far is the ant from its position?
Geometry
Level
pending
The coordinates of ant H and ant K are (-16,18) and (4,2) respectively. Both ants move towards each other on a straight line with different velocities. The velocity of ant H is 3 times the velocity of ant K. What is the distance of ant H from its initial position when it meets with ant K.
The answer is 19.21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Since ant H travels 3 times faster than ant K,then the distance covered by ant H is 3 times the distance travel by ant K.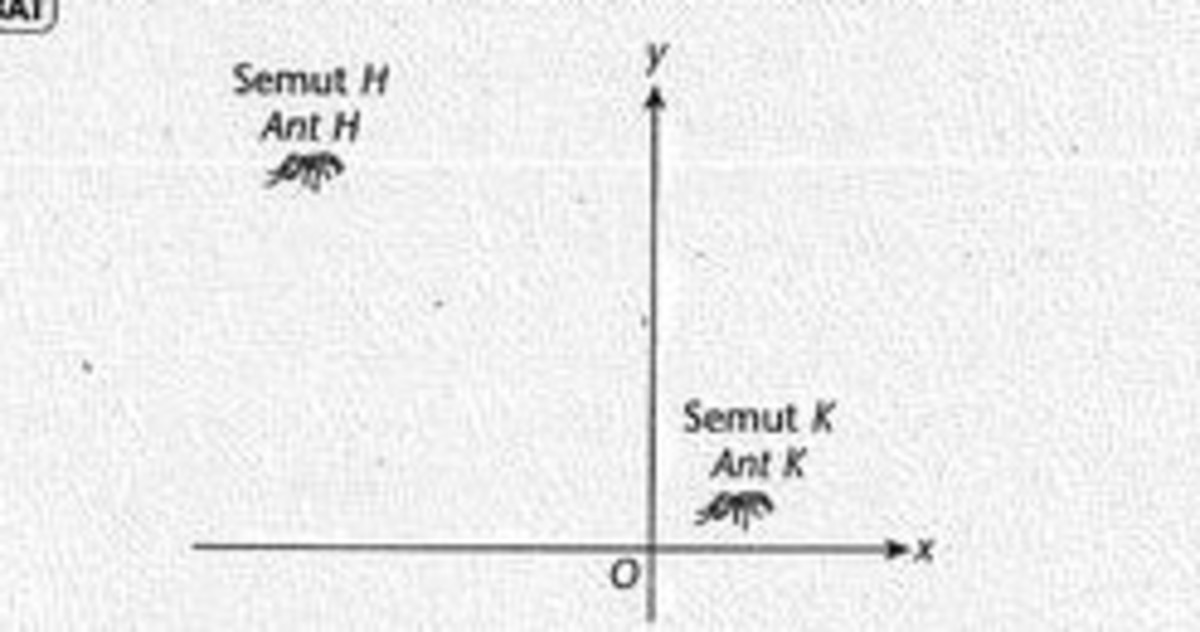
Hence,when both ants meet with each others the ratio distance of ant H to ant K is 3:1. Thus, the equation will be ( 4 1 2 − 1 6 , 4 6 + 1 8 ) =(-1,6)
The ants will meet with each other at point (-1,6). Then use the equation of calculating distance to calculate the distance of ant H d(squared)=225+144, d(squared)=369, d=19.21 units