Making his way to infinity
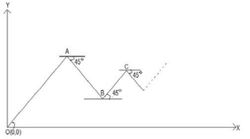 An insect starts moving from the origin,
along the straight line in zig-zag manner. He first moves to
, changes directions and walks half that distance to
, changes direction and walks a further half of the distance to
, so on and so forth.
An insect starts moving from the origin,
along the straight line in zig-zag manner. He first moves to
, changes directions and walks half that distance to
, changes direction and walks a further half of the distance to
, so on and so forth.
If it ultimately ends at a point , then find the value of .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
x = 3 + 3/2 + 3/4 + 3/8 +...
x = 3 + x/2
x = 6
y = 3 - 3/2 + 3/4 - 3/8 +...
y = 3 - 3/2 + y/4
y = 2
So the insect ends up at (6,2). 6 + 2 = 8.