How far should I go ?
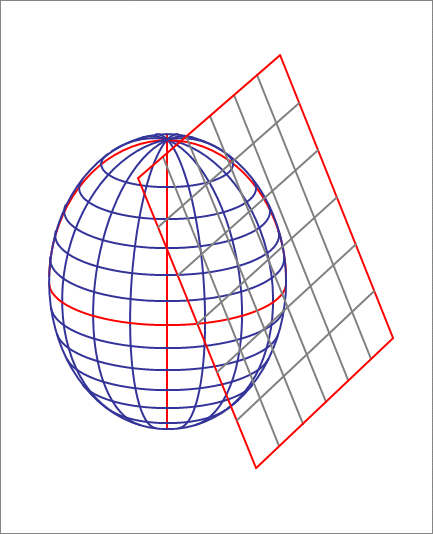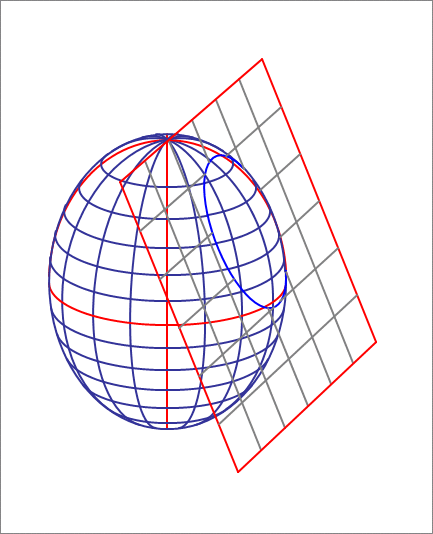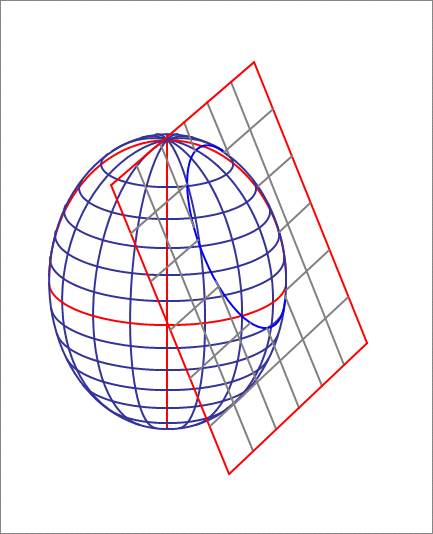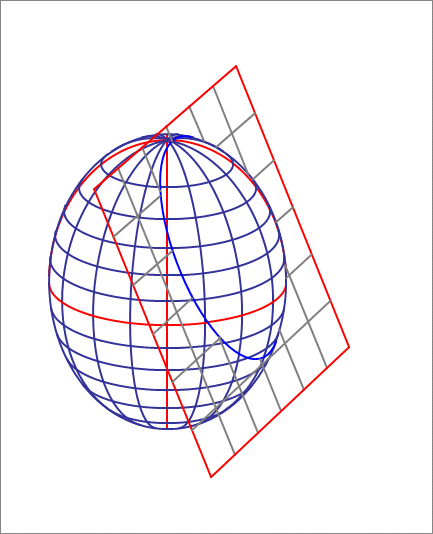
An ellipsoid is described by the equation
A cutting plane has a normal vector equal to . Initially you place the plane tangent to the ellipsoid (in the first octant, where ). Next, you want to move the plane along its normal by a certain distance , such that the area of the ellipse of intersection between the plane and the ellipsoid is units squared. Find .
Note: There are two possible values for . Select the smaller one.
The answer is 6.818.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Define the position vector as r = [ x , y , z ] T , and the diagonal matrix Q = diag [ 1 2 2 1 , 1 5 2 1 , 2 0 2 1 ]
then the equation the ellipsoid can be written as,
r T Q r = 1
Next, let the vector n = 6 1 [ − 1 , − 2 , − 1 ] T be the unit normal vector of the cutting plane.
Then the equation of the cutting plane is n T ( r − r 1 ) = 0 , where r 1 is the position vector of any point on the plane.
We can take r 1 = t n , where t ∈ R is an arbitrary scalar, and the equation of the plane becomes,
n T r = t
If t = 0 , then the cutting plane is at the origin resulting in the maximum possible cut ellipse area.
Let's first find values of t that we will result in the plane being tangent to to the ellipsoid.
If p is the tangency point then from the gradient, Q p = α n , for some α to be determined.
Hence p = α Q − 1 n . Substitute this into the ellipsoid equation, you get, α 2 n T Q − 1 n = 1 , therefore,
α = ± n T Q − 1 n 1
so that, p = ± n T Q − 1 n 1 Q − 1 n
Point p lies on the cutting plane when it is tangent to the ellipsoid, and thus satisfies the plane equation n T r = t . Substituting r = p , gives,
t = n T p = ± n T Q − 1 n 1 n T Q − 1 n = ± n T Q − 1 n
Since we're approaching the ellipsoid from t = − ∞ , we'll take the negative one of these two, i.e. the initial value of t is
t 0 = − n T Q − 1 n
For values of t greater than t 0 and up to t = − t 0 = n T Q − 1 n , we have an intersection between the plane and the ellipsoid.
We want to determine the area of the resulting ellipse of intersection, and for that we'll use the fact that the area of the cut which lies in the cutting plane,
is d t d V ( t ) , where V ( t ) is the volume of the ellipsoid, that is behind the cutting plane. One can see that as t increases,
then so will V ( t ) . To find V ( t ) , we'll transform our ellipsoid into a unit sphere, by using a change of variable r = Q − 2 1 r ′ .
then in terms of r ′ , the equation of our the ellipsoid surface becomes r ′ T r ′ = 1 , which is a unit sphere.
Applying the change of variables to the cutting plane, the equation of the plane becomes, n T Q − 2 1 r ′ = t , which is (in the r ′ space), is a plane whose normal is n ′ = Q − 2 1 n . Note that n ′ is not a unit vector.
The signed distance (along the normal of the plane) between the origin of the sphere and the cutting plane is a = n ′ T n ′ − t = n T Q − 1 n − t
The volume of the sphere lying behind the plane is given by
V s = π ( 3 2 − a + 3 1 a 3 )
Plugging in the expression for a , and introducing c 0 = − t 0 = n T Q − 1 n
V s ( t ) = π ( 3 2 + c 0 t − 3 c 0 3 t 3 )
Now the corresponding volume of the original ellipsoid is
V ( t ) = ∣ Q − 2 1 ∣ V s ( t )
A ( t ) = d t d V ( t ) = ∣ Q − 2 1 ∣ d t d V s ( t ) = ∣ Q − 2 1 ∣ π ( c 0 1 − c 0 3 t 2 )
And this the relation between the cut ellipse area and the parameter t . It is a simple quadratic relation, with maximum at t = 0 , and
two zeros at t = ± c 0 .
Equating A ( t ) to the desired area A 0 = 5 0 0 , and solving for t , (and choosing it to be negative), we get
t 1 = − c 0 1 − ∣ Q − 2 1 ∣ π c 0 A 0
so the required distance is,
d = t 1 − t 0 = c 0 ( 1 − 1 − π a b c c 0 A 0 )
For our ellipsoid and plane normal, one can compute that c 0 = 1 5 . 5 1 3 4 3 5 0 4 , and therefore,
d = 1 5 . 5 1 3 4 3 5 0 4 ( 1 − 1 − ( 1 2 ) ( 1 5 ) ( 2 0 ) π ( 5 0 0 ) ( 1 5 . 5 1 3 4 3 5 0 4 ) ) = 6 . 8 1 8