How fast??

Let's begin by naming a few points: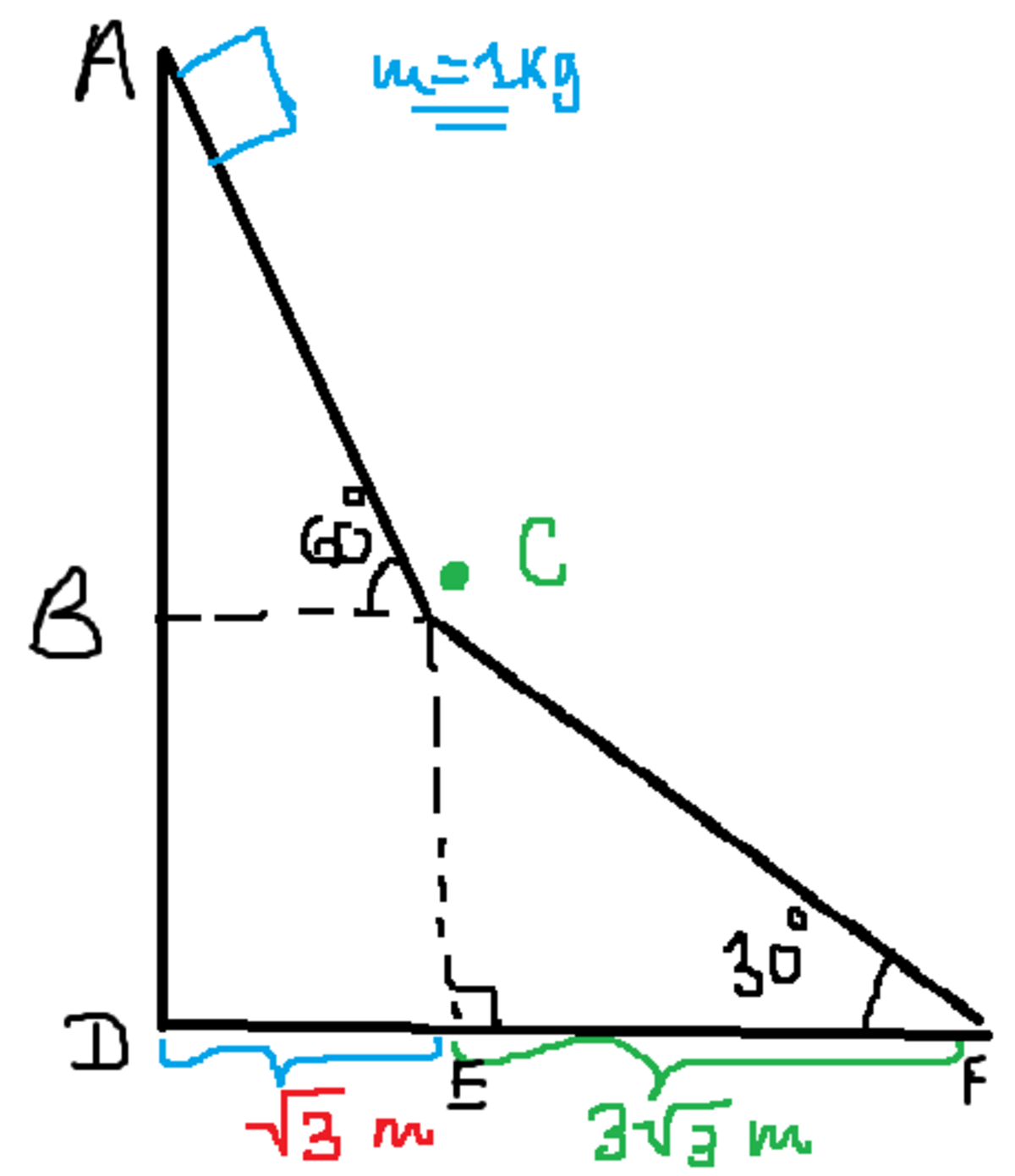

1. Figuring out the height:

In incline CEF:

$CE = EF \times tan(30) = 3\sqrt{3} \times \frac{1}{\sqrt{3}} = 3m$ $BD = CE = 3m$

Similarly in incline ABC:

$BC = DE = \sqrt{3}m$ $AB = BC \times tan(60) = \sqrt{3} \times \sqrt{3} = 3m$

Now, $Height(h) = AB + BD = 3m + 3m = 6m$

2. Figuring out the gravitational potential energy:

$G.P.E(A) = mgh = 1kg \times 10m/s^{2} \times 6m = 60J$

3. Applying the LAW OF CONSERVATION OF MECHANICAL ENERGY:

TOTAL MECHANICAL ENERGY AT A = TOTAL MECHANICAL ENERGY AT C

$=> G.P.E(A) + K.P.E(A) = G.P.E(C) + K.E(C)$

Since, body is placed over the incline K.P.E(A) can be assumed to be 0.

$=> G.P.E(A) = G.P.E(C) + K.E(C)$ $Note: h(C) = CE = 3m. Therefore: G.P.E(C) = mgh(C) = 1kg \times 10m/s^{2} \times 3m = 30J$

Putting in the equation:

$60J = 30J + K.E(C)$ $=> K.E(C) = 30J$

4. USING KINETIC ENERGY TO FIGURE OUT THE SPEED:

Now, Kinetic energy has this neat formula:

$\boxed{ KE = \frac{1}{2} \times m \times v^ {2} }$

Where:

• m -> Mass of object

• v -> Speed of the object

Now, using this formula:

$K.E(C) = \frac{1}{2} \times m \times v^ {2}$ $=> 30J = \frac{1}{2} \times (1 kg) \times v^ {2}$ $=> \frac{2 \times 30J}{1kg} = v^ {2}$ $=> v^ {2} = 60\frac{m^ {2}}{s ^{2}}$ $\boxed{=> v = \sqrt {60} \frac{m}{s}}$