How fast can you do this?
Probability
Level
2
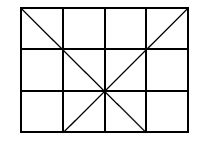
How many triangles are there in the given figure?
29
20
26
27
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
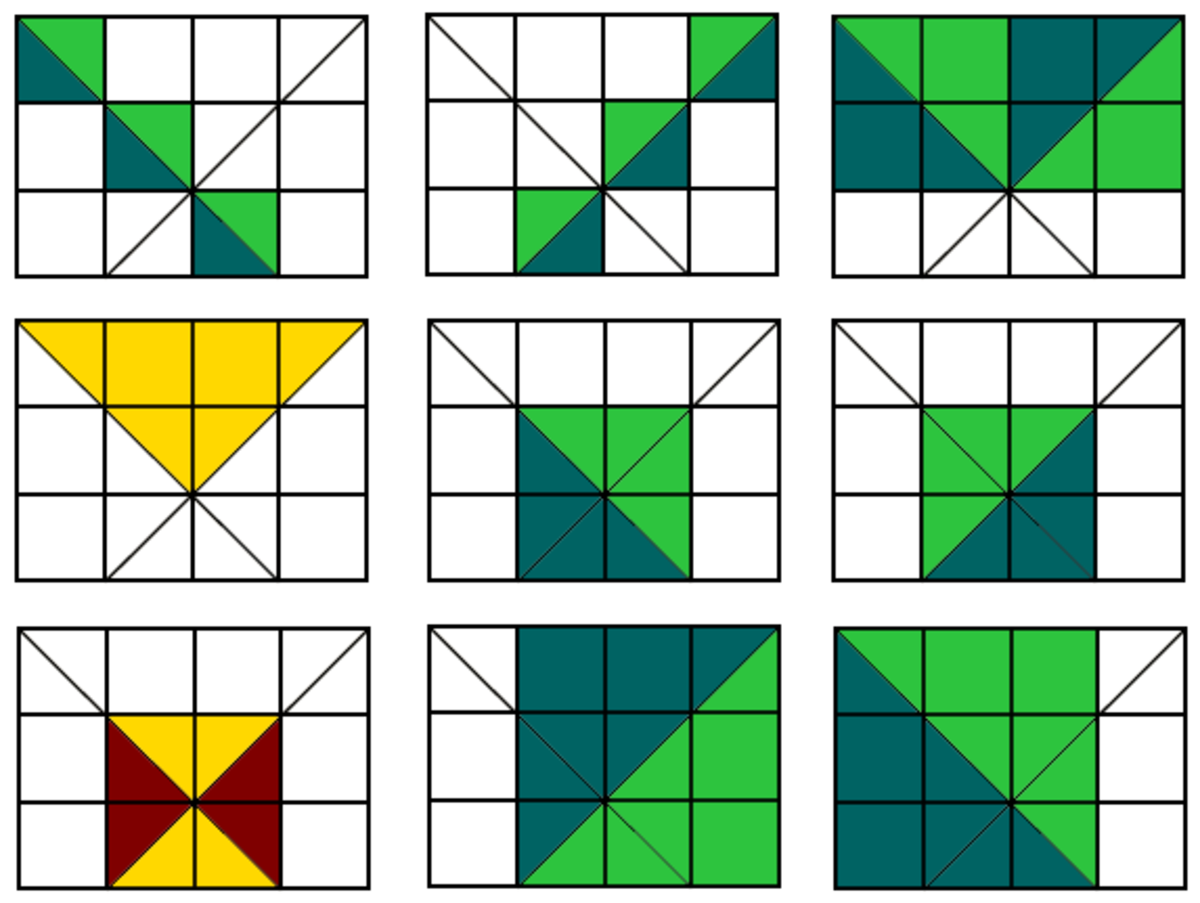
Great puzzle! There are lots of ways to handle the casework, and here's what I did.
Notice that every angle in the figure is either a 9 0 ∘ or a 4 5 ∘ . Therefore, all of the triangles that exist will be 4 5 − 4 5 − 9 0 right triangles. Moreover, the hypotenuse of each triangle will connect the two 4 5 ∘ corners of each triangle. In the figure below, I've labeled points A − G that have 4 5 ∘ angles around them:
Then I considered three cases for the hypotenuses: 1) diagonal lines, 2) vertical lines, 3) horizontal lines.
Using the diagonal lines, there are 12 ways to connect pairs of points on the same horizontal line to create different line segments, and each line segment is the hypotenuse of two triangles (one to each side). The total count is therefore 24.
Additionally, there are 2 triangles which have vertical-line hypotenuses and 3 triangles which have horizontal hypotenuses.
2 4 △ + 2 △ + 3 △ = 2 9 △