Parallelogram Problem
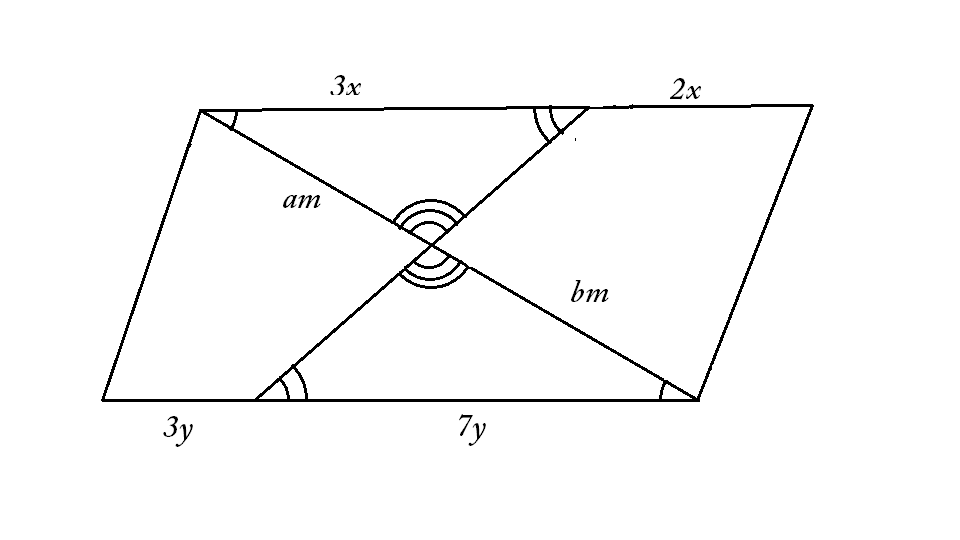
A B C D is a parallelogram. Point P on A B divides it in the ratio A P : P B = 3 : 2 , and point Q on C D divides it in the ratio C Q : Q D = 7 : 3 . Let R be the intersection of P Q and A C . Then, A R : A C = a : b , where a and b are positive coprime integers. What is a + b ?
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
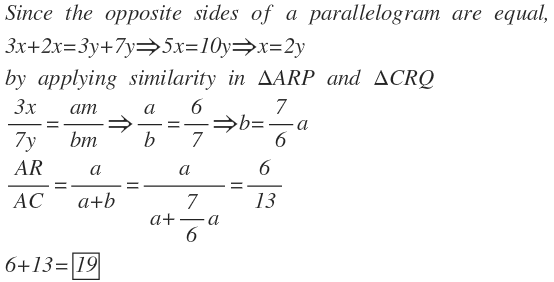
Did it the same way .
If flip the ratio on the lower side :(
From the properties of parallelogram, we can conclude that triangle A P R ∼ C Q R
A P : P B = 3 x : 2 x and C Q : Q D = 7 y : 3 y
Since the 2 opposite sides of a parallelogram are equal, add up the ratios: 3 x + 2 x = 7 y + 3 y and therefore x = 2 y
That means that A P = 3 x = 6 y
Since the 2 triangles are similar, A P : Q C = 6 : 7 , therefore A R = 6 and A C = 6 + 7
T h e s e n u m b e r s n o t t h e a c t u a l l e n g t h s t h e y ′ r e j u s t r a t i o s
A R : A C = 6 : 6 + 7 = 6 : 1 3 = a : b . Thus, a + b = 1 9
The conclusion that, A R = 6 and A C = 1 3 (as ratios ), is not beautiful (opinion). What you intend, is better demonstrated by this property :
A P R ∼ C Q R ⟺ C Q A P = C R A R ⟹ A P + C Q A P = A R + C R A R ⟹ 6 + 7 6 = A C A R
How dumb of me. I was computing A R : R C and getting the answer as 13.
Due to the properties of proportionality, we can treat the parallelogram as a square and solve the problem without affecting the answer.
Therefore, let A B C D be a unit square and their coordinates be A ( 0 , 1 ) , B ( 1 , 1 ) , C ( 1 , 0 ) and D ( 0 , 0 ) , then P ( 0 . 6 , 1 ) and Q ( 0 . 3 , 0 ) .
Then the lines AC and PQ are:
⎩ ⎪ ⎨ ⎪ ⎧ A C : x − 0 y − 1 = 1 − 0 0 − 1 P Q : x − 0 . 3 y − 0 = 0 . 6 − 0 . 3 1 − 0 ⇒ y = 1 − x ⇒ 0 . 3 y = x − 0 . 3 . . . ( 1 ) . . . ( 2 )
Substitute y = 1 − x in equation 2, we get the x -coordinate of R , x R :
⇒ 0 . 3 ( 1 − x R ) = x R − 0 . 3 ⇒ 1 . 3 x R = 0 . 6 ⇒ x R = 1 3 6
If x C is the x -coordinate of C , then we note that A C A R = x C x R = 1 1 3 6 = 1 3 6
⇒ a + b = 6 + 1 3 = 1 9
since its just ratios, we can let AP,PB, DQ, QC be 6,4,3,7 respectively. and then applying similarity on APR and CRQ we get AR/(AC -CR) = 6/7 or AR/AC = 6/7*2 = 12/7 => answer is 12 + 7 = 19
we can easily do the question if we take AB=CD=gcd(2+3,7+3) then AP=18x CQ=21x the solution is now very trivial