How fast do Cars approach each other
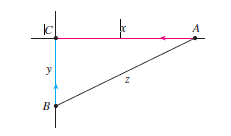
Car A is traveling west at 50 mi/h and car B is traveling north at 60 mi/h. Both are headed for the intersection of the two roads. At what rate are the cars approaching each other when car A is 0.3 mi and car B is 0.4 mi from the intersection? In other words find the rate of change in distance between these cars at the given point.
Give answer as absolute value in mi/h.
The answer is 78.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
By Pythagorean's Theorem on the right triangle given, x 2 + y 2 = z 2 .
By implicit differentiation, 2 x d t d x + 2 y d t d y = 2 x d t d z
Plugging in values x = 0 . 3 , y = 0 . 4 , z = 0 . 3 2 + 0 . 4 2 = 0 . 5 , d t d x = 5 0 , and d t d z = 6 0 gives 2 ( 0 . 3 ) ( 5 0 ) + 2 ( 0 . 4 ) ( 6 0 ) = 2 ( 0 . 5 ) d t d z .
Solving this equation gives d t d z = 7 8 .
Let C the intersection be the origin C ( 0 , 0 ) , the distance from C to car A be x and the distance from C to car B be y . Then rate of change of x or d t d x = − 5 0 , since x is reducing. Similarly, d t d y = − 6 0 . Let the distance between the two cars be s ( x , y ) . Then we have s ( x , y ) = x 2 + y 2 and its rate of change is given by:
d t d s ( x , y ) = ∂ x ∂ s ⋅ d t d x + ∂ y ∂ s ⋅ d t d y = x 2 + y 2 x ( − 5 0 ) + x 2 + y 2 y ( − 6 0 ) = − 0 . 5 0 . 3 ( 5 0 ) − 0 . 5 0 . 4 ( 6 0 ) = − 7 8 Putting x = 0 . 3 and y = 0 . 4
Therefore, the absolute value of rate of change of s at x = 0 . 3 and y = 0 . 4 is 7 8 .
Let x be the distance from car A to the intersection and y be the distance from car B to the intersection. Let z be the distance between the cars. By the Pythagorean theorem, z = x 2 + y 2 . We calculate the derivative of z with respect to time, d t d z :
d t d z = d t d ( x 2 + y 2 ) 2 1 = 2 1 ( x 2 + y 2 ) − 2 1 ( 2 x d t d x + 2 y d t d y ) = 2 1 ( x 2 + y 2 ) − 2 1 ( 2 x ⋅ 5 0 + 2 y ⋅ 6 0 ) = 2 1 ( . 3 2 + . 4 2 ) − 2 1 ( 2 ⋅ . 3 ⋅ 5 0 + 2 ⋅ . 4 ⋅ 6 0 ) = 2 1 . 5 1 ( 3 0 + 4 8 ) = 7 8 d t d x = 5 0 , d t d y = 6 0 Evaluate at ( x , y ) = ( . 3 , . 4 ) . 3 2 + . 4 2 = . 5 2