How good have you studied circles ?

Geometry Level 3

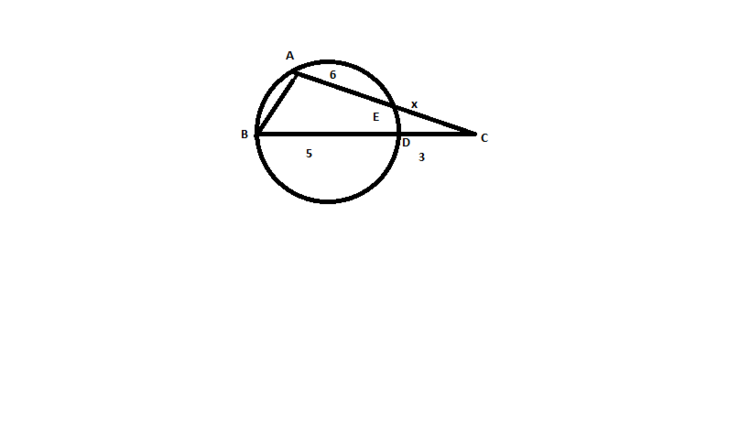The following circle (fig.) has two secants from a common point C, namely AC and BC. The
circumference of the circle intersects these two secants at E and D respectively. If AE = 6 , BD = 5 and DC = 3, then what is the length of seg DC ?


The answer is 2.5.

View wiki
Rajaswa Patil by Rajaswa Patil , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

By the power of a point , we have

C E × E A = C D × D B CE \times EA = CD \times DB

6 x = 3 ( 5 ) 6x = 3(5)

6 x = 15 6x = 15

x = 15 6 = 2.5 x=\dfrac{15}{6}=\boxed{2.5}

0 Helpful 0 Interesting 0 Brilliant 0 Confused
André Meneghetti
Sep 30, 2014

There is a wrong thing about the question, you should ask what is the length of EC. BD times DC must be equal to AE times AC. Then, 15 = 6x; x = 2.5. De boa

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Vishal Oraon
Sep 10, 2014

If two secants intersect in the exterior of a circle, then the product of measures of the segments the intersection point divides each chord is same.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

1 pending report

Vote up reports you agree with

×

Problem Loading...

Note Loading...

Set Loading...