How harmonic!

$\begin{aligned} \frac 1a + \frac 1b & = \frac 15 + \frac 15 \\ \frac {\color{#3D99F6}a+b}{ab} & = \frac 25 & \small \color{#3D99F6} \text{Note that } a+b = 5+5 = 10 \\ \frac {10}{ab} & = \frac 25 \\ \implies ab & = 25 = \boxed{5 \times 5} \end{aligned}$

We have the following system of equations

$\begin{cases} a+b=10\\ \dfrac{1}{a}+\dfrac{1}{b}=\dfrac{2}{5} \end{cases} \iff \begin{cases} b=10-a\\ 5a+5b=2ab \end{cases}$

Substituting $b$ in the second equation and solving for $a$

$5a+5(10-a)=2a(10-a)$

$a^2-10a+25=0$

$(a-5)^2=0 \iff a=5$

Which implies $b=10-5=5$ , making $\boxed{(a,b)=(5,5)}$ the only solution

$\frac{1}{a}$ + $\frac{1}{b}$ = $\frac{1}{5}$ + $\frac{1}{5}$

or, $\frac{a+b}{ab}$ = $\frac{2}{5}$

or, $2ab=50$ ......................................[a+b=5+5=10]

or, $ab=25$ = $5 \times 5$

$\begin{aligned} \dfrac 1a + \dfrac 1b & = \dfrac 15 + \dfrac 15 \\ \dfrac{a+b}{ab} & = \dfrac 25 \\ \dfrac{5+5}{ab} &= \dfrac 25 \\ 2ab & = 50 \\ ab & = \dfrac{50}{2} \\ ab & = \boxed{25} \\ \end{aligned}$

(1) $a + b = 5 + 5$

(2) $\frac{1}{a}$ + $\frac{1}{b}$ = $\frac{1}{5}$ + $\frac{1}{5}$ ==> $\frac{a + b}{ab}$ = $\frac{5 + 5}{5 * 5}$

Divide equation (1) by equation (2)

$\frac{(1)}{(2)} ==>\frac{a + b}{\left({\displaystyle\frac{a+b}{ab}}\right)} = \frac{5 + 5}{\left({\displaystyle\frac{5+5}{5*5}}\right)}$

$\frac{(1)}{(2)} ==>\frac{(a + b)(ab)}{\left({a+b}\right)} = \frac{(5 + 5)(5*5)}{\left({5+5}\right)}$

$ab = 5*5$

$\dfrac{a+b}{2}=\dfrac{2}{\dfrac{1}{a}+\dfrac{1}{b}}$

It is AM-HM inequality equality case

$\therefore a=b=5$

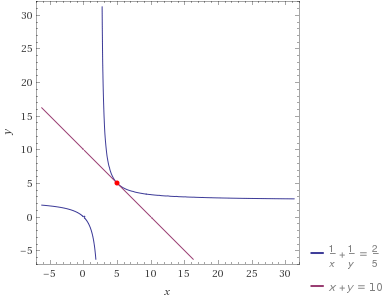Plotting the two equations reveals that they only intersect at (5,5)

Just multiply the second equation by $ab$ . $a + b = \frac{2ab}5$ and substitute for $a + b$ as per the first equation $10 = \frac{2ab}5 \\ \Rightarrow ab = 25$

1/a+1/b=2/5=40%. a+b=10 1/3=33.33% 1/7=14.28% 1/4=25% 1/6=16.66% 1/2=50% Only combination which equals 40% is 1/5+1/5 So a and b are both 5

isn't it just apparent that the equations demonstrate that a=5 and b=5? This requires no algebra at all just recognition of the meaning of the terms demonstrated.

$a + b = 5 + 5 \implies a = 10 - b \implies \dfrac{1}{10 - b} + \dfrac{1}{b} = \dfrac{2}{5} \implies$

$50 = 20b - 2b^2 \implies b^2 - 10b + 25 = 0 \implies (b - 5)^2 = 0 \implies b = 5 \implies a = 5$

$\therefore a\times b = 5\times5$