How high can you lift?
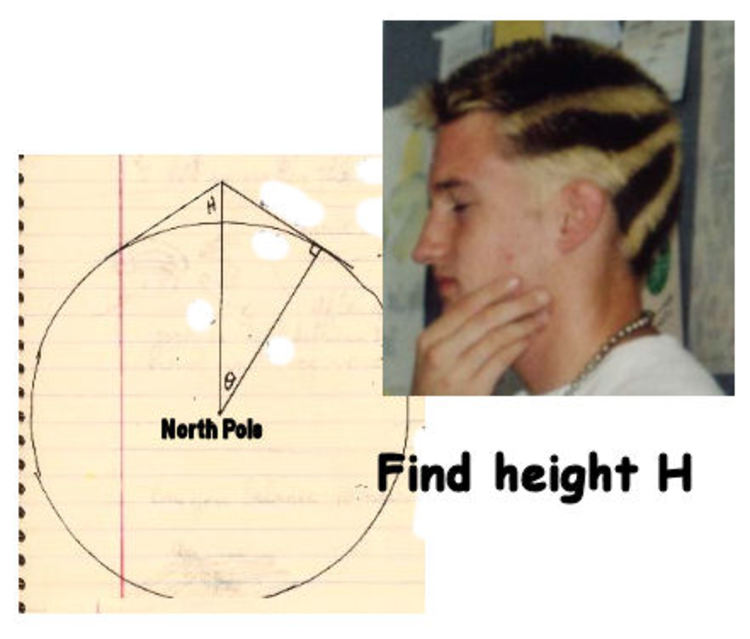A length of wire completely surrounds the earth at the Equator. Imagine that the wire floats, that it has negligible mass, and that it fits snugly around the earth. Cut the wire and splice in an extra 20 feet of wire. Now the wire will be slightly slack in its fit. Raise the wire at one point until the wire is taut again. How high can you lift it? (answer correct to nearest foot)
Take the radius of the earth as 20,903,520 feet.
The answer is 1330.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I think that solving that equation is the real problem
L e t H b e t h e r e q u i r e d h e i g h t , a n d R = 2 0 9 0 3 5 2 0 f e e t . A f t e r l i f t i n g t h r o u g h H , t h e r e w i l l b e T a n g e n t f r o m t h i s h e i g h t . L e t t h e r a d i u s f r o m p o i n t o f t a n g e n c y a n d H + R l i n e f r o m t o p o f h t o c e n t e r m a k e a n a n g l e α r a d i a n . ∴ t h e t a n g e n t l e n g t h = ( A r c l e n g t h + 2 0 / 2 ) = ( α ∗ R + 2 0 / 2 ) . B u t t h e t a n g e n t l e n g t h a l s o = T a n ( α ) ∗ R . ⟹ α ∗ R + 2 0 / 2 = T a n ( α ) ∗ R , ⟹ R ( T a n ( α ) − α ) − 1 0 = 0 . P l o t t i n g t h i s c u r v e i n a g r a p h i n g c a l c u l a t o r a n d r e f i n i n g b y t r i a l a n d e r r o r , α = 0 . 0 1 1 2 8 . ( H + R ) ∗ C o s ( α ) = R . S o l v i n g , H = 1 3 2 9 . 9 3 . . . ≈ 1 3 3 0 .
you have good writing , but I have same solution... :)
Length of Arc + 20 = Length of tangents.
2 ∗ t h e t a ∗ r a d i u s + 2 0 = 2 r ∗ t a n ( t h e t a )
radius of earth in feet = 2 0 , 9 0 3 , 5 2 0 f t
solving the equation, we get t h e t a = 0 . 6 4 6 2 7 3 d e g r e e s
c o s ( t h e t a ) = r / ( r + h ) , thus h = 1 3 3 0 f t .