How high is the highest point ?
An ellipse with a semi-major axis length of 2 0 units and a semi-minor axis length of 1 0 units, is to be placed in the first quadrant such that it is tangent to the x -axis and the y -axis and the line x = 3 0 . How high (above the x -axis) is the highest point on this ellipse ?
The answer is 33.166.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I didn't get symmetry. Will you elaborate?
Log in to reply
The center of the ellipse is the midpoint of the points with extreme x-coordinates, that is, the points with the maximum x-coordinate and the point with minimum x-coordinate.
Below is a formula for a generalized 2D ellipse. The ellipse center is at ( x 0 , y 0 ) . Its semi-major and semi-minor axis lengths are a and b , and the major axis is oriented at an angle θ with respect to the positive x axis.
A x 2 + B x y + C y 2 + D x + E y + F = 0 A = a 2 sin 2 θ + b 2 cos 2 θ B = 2 ( b 2 − a 2 ) sin θ cos θ C = a 2 cos 2 θ + b 2 sin 2 θ D = − 2 A x 0 − B y 0 E = − B x 0 − 2 C y 0 F = A x 0 2 + B x 0 y 0 + C y 0 2 − a 2 b 2
When x = 0 , and assuming that there is only one corresponding y value:
C y 2 + E y + F = 0 ⟹ E 2 − 4 C F = 0
When y = 0 , and assuming that there is only one corresponding x value:
A x 2 + D x + F = 0 ⟹ D 2 − 4 A F = 0
When x = x ′ = 3 0 , and assuming that there is only one corresponding y value:
A x ′ 2 + B x ′ y + C y 2 + D x ′ + E y + F = 0 ⟹ ( B x ′ + E ) 2 − 4 C ( A x ′ 2 + D x ′ + F ) = 0
After numerical solution, the values which satisfy these equations are:
x 0 ≈ 1 5 . 0 0 0 y 0 ≈ 1 6 . 5 8 3 θ ≈ 4 9 . 7 9 7 ∘
The highest point occurs at y ≈ 3 3 . 1 6 6 .
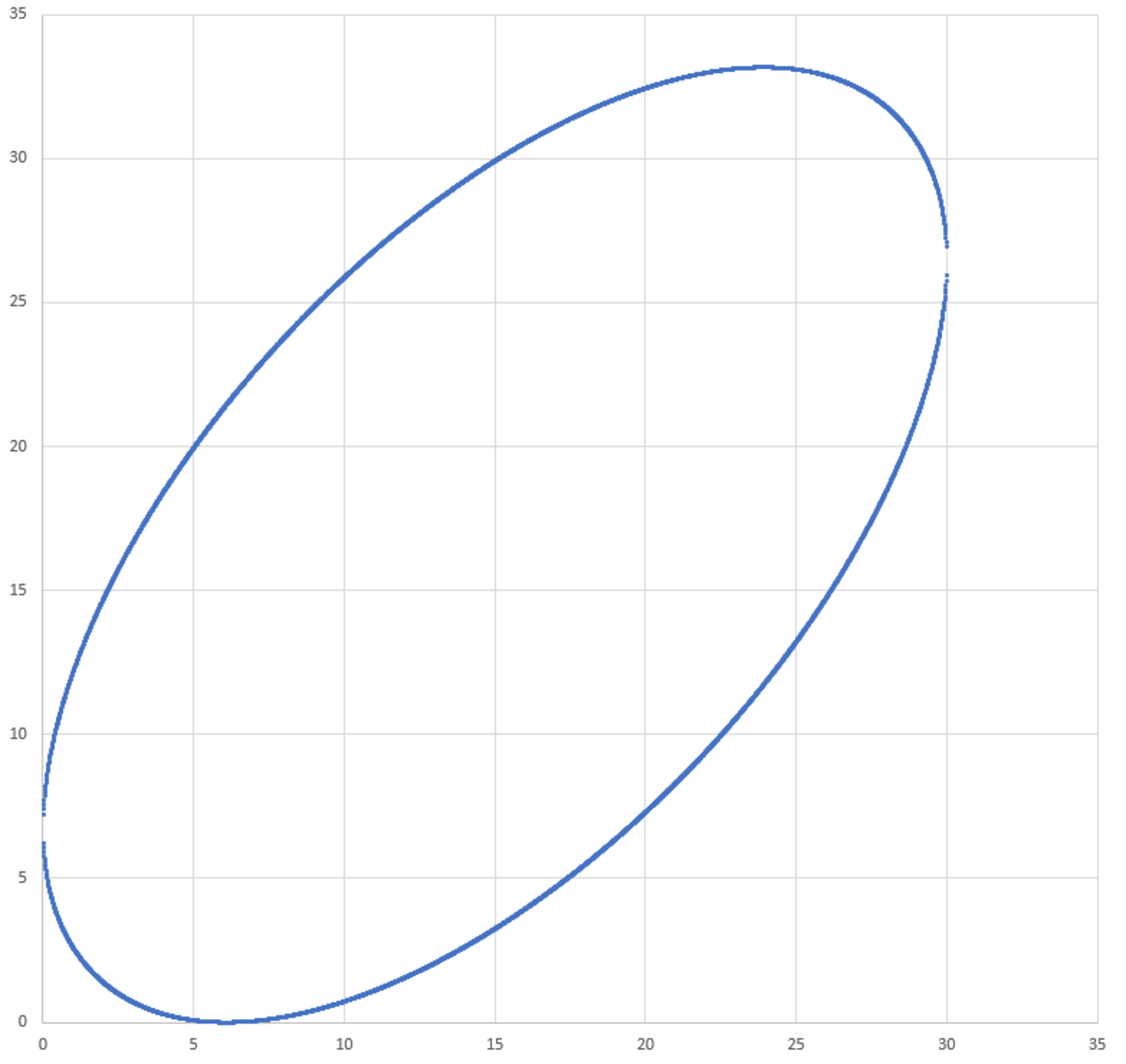
The simple way to go about solving this problem is using the fact that an ellipse with semi-axes a , b that is tangent to both the x and y axes, has its center C = ( C x , C y ) satisfying
C x 2 + C y 2 = a 2 + b 2
Now, from symmetry, we know that C x = 2 3 0 = 1 5 , hence C y = 1 0 0 + 4 0 0 − 2 2 5 = 2 7 5 . And using the symmetry argument again, it follows that the highest point y -coordinate is H = 2 C y = 2 2 7 5 = 3 3 . 1 6 6