How high must I fill?
A conical frustum cup with bottom radius 2 and top radius 4 and vertical height 1 0 , is to be filled to half the cup's capacity with water. How high should I fill it with water? Find the height of the water line above the bottom base.
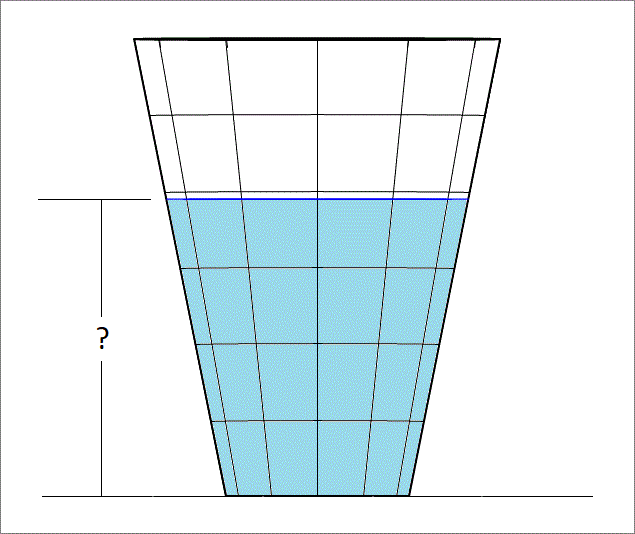
The answer is 6.5096.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The picture seems to be drawn to scale.
Extend the sides of the frustum to form a triangle at the bottom (and hence a right circular cone). If H is the height of this triangle, similar triangles shows:
2/H = 4 / (H+10)
Solving yields
H = 10.
We then have two cones formed (a "big" one with radius 4 and height 20 and a "small" one with radius 2 and height 10). Utilizing the formula for the volume of a right circular cone:
Volume of frustum = Volume of "big" right cone - volume of "small" cone = (Pi/3) (4^2) 20 - (Pi/3) (2^2) 10
Volume of frustum = 280*Pi/3 (equation 1)
After the water is filled, let the radius be r and the height of the water above the bottom of the frustum be h. Using similar triangles again, we find:
r/(h+10) = 2/10, or
h = 5*r-10 (equation 2)
Again, subtracting volumes yields:
Volume of water = Pi (r^2) (h+10) / 3 - (Pi/3) (2) (2) 10 = (1/2) 280*Pi/3 (the last equation follows from equation 1 and the fact that the volume of water is 1/2 the volume of the frustum).
Now, substitution equation 2 into this and simplifying yields:
5*r^3 = 180
or, r = (36)^(1/3) and h = 5*(36^(1/3)) - 10 = 6.5096 (approximately)
Let the bottom radius, the top radius and the height of the conical frustum be r , R , H respectively, and let the required height be H ′ .
Then,
H ′ = H × R − r ( 2 R 3 + r 3 ) 3 1 − r
Substituting values we get
H ′ = 5 × ( 3 6 3 1 − 2 ) ≈ 6 . 5 0 9 6 .
Extend the sides of the frustrum as follows. Then the larger cone and the smaller cone are similar by A A . By similar triangles, h 2 = h + 1 0 4 ⇒ h = 1 0 .
Now, V ∝ L 3 , so the volume is proportional to any of the lengths cubed. Let the volume of the entire cone be V . Then the volume of the frustrum can be expressed as (large cone - small cone), and the volume of the small cone can be represented as ( large cone radius small cone radius ) 3 V : a proportion of the large cone's volume. Thus the frustrum's volume is V − ( 4 2 ) 3 V = 8 7 V , so the volume of the water is 1 6 7 V .
We use similarity again but in terms of the heights. ( 2 0 1 0 + h ) 3 V − ( 2 0 1 0 ) 3 V = 1 6 7 V . Cancelling the V s and rearranging gives ( 2 0 1 0 + h ) 3 = 1 6 7 + 8 1 , and so 1 0 + h = 2 0 ( 1 6 7 + 8 1 ) 1 / 3 ⇒ h ≈ 6 . 5 0 9 6 .