How is this a geometry problem?

Geometry Level 2

What is the value of $x$ that minimizes $\sqrt{(4-x)^{2} + 25} + \sqrt{(2-x)^{2}+25}?$

The answer is 3.

3 solutions

Ujjwal Rane
Aug 27, 2015

The resemblance of the two terms to distance formula is unmistakable!

With that in mind, it starts looking like minimizing the distance of a point P from two other points A(2,0) and B(4,0) . Also, the y coordinate of P must be 5 (or -5 just as well). So y = 5 is the locus of P.

Now, distance of a point from two other points remind us of an ellipse being drawn with a string and two pins!. The pins will be at A and B, making then the foci. The figure shows this ellipse by red dotted line. Three random 'string positions' are also shown.

The problem now reduces to: Using A and B as foci draw the SMALLEST ellipse that goes through a point on Y = 5.

For shortest string, Y = 5 must be a tangent to that ellipse. Giving us the point of tangency T to be (3,5) by symmetry.

And this is nothing but the point we are looking for on on y = 5.

So P = T = (3,5) Yielding x = 5

Imgur Imgur

Moderator note:

This geometric interpretation is nice, but slightly complicated to set up.

There is a simpler geometric interpretation, where we express it as distance $AX + XB$ where $A = (2, 5), B = (4, -5)$ and $X = (x,0)$ lies on the x-axis. It then becomes immediately clear that we want the straight-line distance, which is minimized at $X = (3,0)$ .

Thank you for the valuable feedback Challenge Master!

Ujjwal Rane - 5 years, 9 months ago

Sean Sullivan
Jul 28, 2015

Let $f(x)=\sqrt{(4-x)^{2} + 25}$ and $g(x)=\sqrt{(2-x)^{2}+25}$

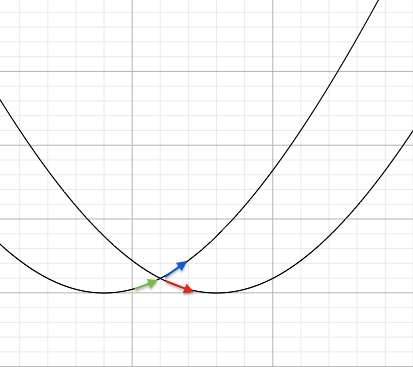
Note that each section of the sum is the upper half of a hyperbola, $f(x)$ is symmetric about $x=4$ and $g(x)$ about $x=2$ , and they are congruent.

Horizontal symmetry of hyperbolas tells us that, as they are congruent they will intersect at $x=\frac{4+2}{2}=3$ .

Since they are symmetric, the increase in $g(x)$ represented by the green arrow is the addititive inverse of the decrease in $f(x)$ represented by the red arrow. As they are concave up, the blue line in the picture will increase at a faster rate than the green line increases and by transitive logic, the blue line will increase faster than the red line decreases, thus, moving out from $x=\boxed{3}$ in either direction yields a larger sum for $f(x)$ and $g(x)$ .

Pranshu Malik
Jul 28, 2015

Pythagoras triangle, and see which summation of hypotenuse gives the least answer, given the fixed altitude or base of 5 units.

Could you please explain?

Omkar Kulkarni - 5 years, 10 months ago

Here's my thinking process when I wrote the problem. First, we notice that the expression for $x$ is very similar to the distance formula for two points. Just as a reminder, if you have points $A(m, n)$ and $B(p, q)$ , then the distance between them is $\sqrt{(m-p)^{2}+(n-q)^{2}}$ .

After this observation, the problem can be reduced to minimizing $AC+BC$ , where $A$ , $B$ and $C$ are points on the plane that we need to figure out next. Let's say $x$ is the $x$ coordinate of point $C$ . Then we can also guess the $x$ coordinate of $A$ is $4$ and the $x$ coordinate of $B$ is $2$ . Since $25=5^{2}$ or $(-5)^{2}$ , we can then say that the $y$ coordinate of point $C$ is $5$ , the $y$ coordinate for point $A$ is $10$ and the $y$ coordinate for point $B$ is $0$ . (This is not the only possible values for points $A$ , $B$ and $C$ , but it is one of the most obvious ones. Other values work, but for some, you will have to reflect $A$ or $B$ over $y = a$ , where $a$ is the $y$ coordinate of point $C$ .) Now, we can work with $AC+BC$ .

$AC=\sqrt{(4-x)^{2}+(10-5)^{2}}=\sqrt{(4-x)^{2}+25}$ . $BC = \sqrt{(2-x)^{2}+(0-5)^{2}} = \sqrt{(2-x)^{2}+25}$ . Summing these together results in the expression in the problem.

We have now taken the original statement and converted it into this: find the value of $x$ that minimizes $AC+BC$ where point $A$ is $(4, 10)$ , point $B$ is $(2, 0)$ and point $C$ is $(x, 5)$ . Try plotting these points on a plane. You might draw first line $y = 5$ (this is the set of all possible points $C$ ), then below it, point $B$ , and finally above it, point $A$ . Point $C$ must lie on segment $AB$ , since the shortest distance between two points is a straight line. This minimizes the expression. The slope of the line that runs through $A$ and $B$ is $\frac {10-0}{4-2} = 5$ . The line that runs through points $A$ and $B$ is $y = 5 x-10$ . We can find where this line intersects line $y = 5$ by solving for $x$ in the equation $5 = 5x-10$ . We will get the answer $\boxed{x=3.}$ .

This problem can be solved in about two seconds with the AM-GM inequality, but it's always fun finding weird solutions to problems.

Steven Mai - 5 years, 10 months ago

Had a problem on a contest once and the only way to solve it was to make that intriguing observation :D I really think that such geometric apraoch to algebraic problems are wonderfull gj

Rohan Nuckchady - 5 years, 10 months ago

Ohh right. Amazing idea! Hats off. Thanks!

Omkar Kulkarni - 5 years, 10 months ago

How is this a geometry problem?

The answer is 3.

3 solutions

Moderator note:

0 pending reports