How is this calculus?

Calculus Level 5

Suppose that a , b , c a, b, c are real numbers chosen independently at random from the interval [ 0 , 1 ] [0, 1] . What is the probability that the polynomial a x 2 + b x + c ax^2+bx+c has real roots?


The answer is 0.2544.

View wiki
Alex Li by Alex Li , 22, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The probability of Case 1 and 2 combined would be multiplied by 1 4 \frac{1}{4} because we are selecting the region of [ 0 , 0.25 ] [0,0.25] out of [ 0 , 1 ] [0,1] and for case 3 the probability would be multiplied by 3 4 \frac{3}{4} because we are selecting the region from ( 0.25 , 1 ] (0.25,1] out of [ 0 , 1 ] [0,1] . That would give the final value as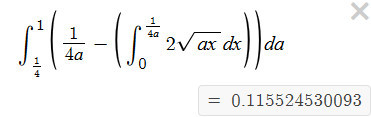 Add them to get 0.254413 0.254413

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...