How is this possible ?

Geometry Level pending

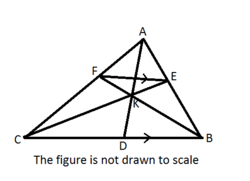D, E and F are lying on the sides BC, AB and AC respectively of a triangle ABC right angled at A. Suppose AD, CE and BF intersect at point K and FE is parallel to CB. It is given that AD=5 ,then find the length of CB

The answer is 10.

1 solution

Divyansh Chaturvedi
Dec 3, 2014

Since D, E, and F are general points, assume them to be the the midpoints of respective sides. So AD = 1/2 of CB. So, BC is 10

That's no solution. You will have to prove AD=DB for all cases. K cannot be assumed as the centroid of the triangle ABC.

Rayyan Shahid - 6 years, 6 months ago

Easy. Basically, parallelism of FE to BC means: Similiarity of $\Delta ABC$ and $\Delta AEF$ $\implies$ $\frac{AE}{EB} = \frac{AF}{FC}$ ...(1)

Now use Ceva's theorem for $\Delta ACB$ :

$\frac{CF}{FA} \times \frac{AE}{EB} \times \frac{BD}{DC} = 1$

$\implies (using (1)) BD = DC$

So, $AD$ is the median.

Now then, in the right triangle, the median from the right angled vertex is half the hypotenuse.

So, hypotenuse is $10$ .

Ashutosh Kumar - 6 years, 5 months ago

How is this possible ?

The answer is 10.

1 solution

0 pending reports