How is this possible?
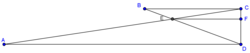 In the figure,
,
,
,
and
. If
is the minimal monic polynomial with integer coefficients which has
as one of its roots, find
.
In the figure,
,
,
,
and
. If
is the minimal monic polynomial with integer coefficients which has
as one of its roots, find
.
The answer is 1024.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let A D = a , B C = b , D F = x − c and F C = c . Triangles △ D F E and △ D C B are similar, hence 2 x − c = b x . And triangles △ C F E and △ C D A are also similar, hence 2 c = a x .
Adding those two equations we get:
2 x = a x + b x ⟹ 2 1 = a 1 + b 1
Now apply Pythagorean Theorem on triangles △ C D A and △ D C B :
a 2 + x 2 = 4 9 ⟹ a = 4 9 − x 2
b 2 + x 2 = 9 ⟹ b = 9 − x 2
Susbtitute a and b on the first equation:
2 1 = 4 9 − x 2 1 + 9 − x 2 1
Multiply both sides by 2 4 9 − x 2 9 − x 2 :
x 4 − 5 8 x 2 + 4 4 1 = 2 ( 4 9 − x 2 + 9 − x 2 )
Square both sides:
x 4 − 5 8 x 2 + 4 4 1 = 4 ( 5 8 − 2 x 2 + 2 x 4 − 5 8 x 2 + 4 4 1 )
x 4 − 5 0 x 2 + 2 0 9 = 8 x 4 − 5 8 x 2 + 4 4 1
Square both sides again, simplify, equate to 0 and find the polynomial:
x 8 + 2 5 0 0 x 4 + 4 3 6 8 1 − 1 0 0 x 6 + 4 1 8 x 4 − 2 0 9 0 0 x 2 = 6 4 x 4 − 3 7 1 2 x 2 + 2 8 2 2 4
x 8 − 1 0 0 x 6 + 2 8 5 4 x 4 − 1 7 1 8 8 x 2 + 1 5 4 5 7 = 0
P ( x ) = x 8 − 1 0 0 x 6 + 2 8 5 4 x 4 − 1 7 1 8 8 x 2 + 1 5 4 5 7
This polynomial is irreducible, hence P ( 1 ) = 1 0 2 4 .