How Long Can Life Last in This Simulation

Computer Science Level 2

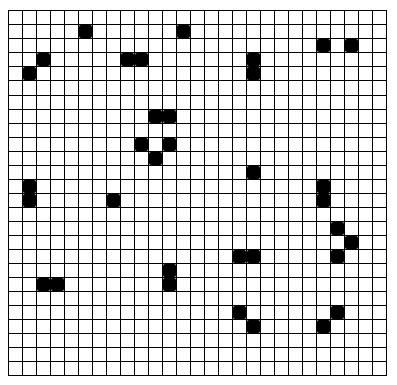Conway's Game of Life is a simple algorithm that produces complex and often beautiful results. It is played on a grid and follows the rules below.

  • Any live cell with fewer than two live neighbors dies, simulating under-population.
  • Any live cell with two or three live neighbors lives on to the next generation.
  • Any live cell with more than three live neighbors dies, simulating overcrowding.
  • Any dead cell with exactly three live neighbors becomes a live cell, simulating reproduction.

If the grid above is generation 1, what is the number of the last generation with living cells?

Details and assumptions

Every cell not on the edges of the grid has 8 8 neighbors: namely, any cell that is horizontally, vertically, or diagonally adjacent.

A generation constitutes one simultaneous application of the rules to every cell in the grid.

If you are interested in the idea of self-organization, you might also like this problem .

2 1 3 4

View wiki
Chung Gene Keun by Chung Gene Keun , 42, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Oscar Fonseca
Jan 25, 2014

Perhaps not the most elegant way to solve it, but I think it is quite straightforward, in C/C++. #include <stdio.h> 

int grid[27][27] = {0};
int adjacents[27][27] = {0};
int live = 0, last = 0, gen = 1;

int checkcon(int, int);

int main () {
    grid[1][5] = 1;
    grid[1][12] = 1;
    grid[3][2] = 1;
    grid[3][8] = 1;
    grid[3][9] = 1;
    grid[3][17] = 1;
    grid[4][1] = 1;
    grid[4][17] = 1;
    grid[7][10] = 1;
    grid[7][11] = 1;
    grid[9][9] = 1;
    grid[9][11] = 1;
    grid[10][10] = 1;
    grid[11][17] = 1;
    grid[12][1] = 1;
    grid[12][22] = 1;
    grid[13][1] = 1;
    grid[13][7] = 1;
    grid[13][22] = 1;
    grid[15][23] = 1;
    grid[16][24] = 1;
    grid[17][16] = 1;
    grid[17][17] = 1;
    grid[17][23] = 1;
    grid[18][11] = 1;
    grid[19][2] = 1;
    grid[19][3] = 1;
    grid[19][11] = 1;
    grid[21][16] = 1;
    grid[21][23] = 1;
    grid[22][17] = 1;
    grid[22][22] = 1;

    int cond = 0;
    do{
        last = live;
        live = 0;
        for(int i = 0; i < 27; i++){
            for(int j = 0; j < 27; j++){
                adjacents[i][j] = checkcon(i, j);
                if(grid[i][j])
                    live++;
                //printf("%i", grid[i][j]);
            }
            printf("\n");
        }

        printf("\n");

        for(int i = 0; i < 27; i++){
            for(int j = 0; j < 27; j++){
                if(grid[i][j]) {
                    if(adjacents[i][j] < 2 || adjacents[i][j] > 4)
                        grid[i][j] = 0;
                    else
                        grid[i][j] = 1;
                } else {
                    if(adjacents[i][j] == 3)
                        grid[i][j] = 1;
                    else
                        grid[i][j] = 0;
                }
            }
        }
        gen++;
        printf("====gen %i, alive %i====\n", gen, live);
    }while(live);

    printf("last generation %i\n", last);
    return 0;
}

int checkcon(int x, int y) {
    int neigh = 0;
    if(x == 0 && y == 0) {
        //printf("e");
        if(grid[x][y+1])
            neigh++;
        if(grid[x+1][y])
            neigh++;
        if(grid[x+1][y+1])
            neigh++;
    } else if(x == 0 && y == 26) {
        //printf("e");
        if(grid[x+1][y])
            neigh++;
        if(grid[x+1][y-1])
            neigh++;
        if(grid[x][y-1])
            neigh++;
    } else if(x == 26 && y == 26) {
        //printf("e");
        if(grid[x-1][y-1])
            neigh++;
        if(grid[x-1][y])
            neigh++;
        if(grid[x][y-1])
            neigh++;
    } else if(x == 26 && y == 0) {
        //printf("e");
        if(grid[x-1][y+1])
            neigh++;
        if(grid[x-1][y])
            neigh++;
        if(grid[x][y+1])
            neigh++;
    } else if(x == 0) {
        //printf("t");
        if(grid[x][y+1])
            neigh++;
        if(grid[x][y-1])
            neigh++;
        if(grid[x+1][y+1])
            neigh++;
        if(grid[x+1][y-1])
            neigh++;
        if(grid[x+1][y])
            neigh++;
    } else if(x == 26) {
        //printf("b");
        if(grid[x][y+1])
            neigh++;
        if(grid[x][y-1])
            neigh++;
        if(grid[x-1][y+1])
            neigh++;
        if(grid[x-1][y-1])
            neigh++;
        if(grid[x-1][y])
            neigh++;
    } else if(y == 0) {
        //printf("l");
        if(grid[x][y+1])
            neigh++;
        if(grid[x-1][y+1])
            neigh++;
        if(grid[x-1][y])
            neigh++;
        if(grid[x+1][y+1])
            neigh++;
        if(grid[x+1][y])
            neigh++;
    } else if(y == 26) {
        //printf("r");
        if(grid[x][y-1])
            neigh++;
        if(grid[x-1][y-1])
            neigh++;
        if(grid[x-1][y])
            neigh++;
        if(grid[x+1][y-1])
            neigh++;
        if(grid[x+1][y])
            neigh++;
    } else {
        //printf("m");
        if(grid[x][y+1])
            neigh++;
        if(grid[x][y-1])
            neigh++;
        if(grid[x-1][y+1])
            neigh++;
        if(grid[x-1][y-1])
            neigh++;
        if(grid[x-1][y])
            neigh++;
        if(grid[x+1][y+1])
            neigh++;
        if(grid[x+1][y-1])
            neigh++;
        if(grid[x+1][y])
            neigh++;
    }

    printf("%i", neigh);
    return neigh;
}
6 Helpful 0 Interesting 0 Brilliant 0 Confused

One could also solve this by hand.

Arman Siddique - 7 years, 4 months ago

Log in to reply

Yup. Just "play out" the round using your own knowledge of how the game works. Since it only lasts between 2-5 rounds (as the multiple choice answers imply), it's not very hard to do so.

Michael Tong - 7 years, 4 months ago

Lol that's what I did while marveling at my beautiful pictures of you and doing my English Complex Process

William Cui - 7 years, 4 months ago

Don't you think there's a faster way to do that? I mean, it's great, but remember, beautiful code is code that's short and to the point. Otherwise you miss the point of "code": making processes that are usually hard to solve easy by giving it to the computer.

Finn Hulse - 7 years, 4 months ago

Still, I'm not sure how you would be able to handle all the 9 cases for cells, keep track of the adjacent tiles without instantly killing or making cells, and giving the input in a simple manner. If you have a better solution, please show it.

Oscar Fonseca - 7 years, 4 months ago

Log in to reply

I dont know if this is necessarily better but I have some code I made a quite a while back that animates the Game of life using a python gaming library called pygame .For this problem,you will have to enter the grid in the self.Grid variable. Here is the code: The indentation should adjust when you copy it to an IDE 

import copy
import pygame
from pygame.locals import Rect,QUIT
from sys import exit
from random import choice

class game_of_life:
    '''Implements Conways's Game of Life with Pygame'''

    def __init__(self,size):
        self.time = 0
        self.screen = pygame.display.set_mode(size[0],0,32)
        self.size ,self.whole = size[0][0] / size[1] , size
        self.draw_grid()
        #self.Grid = [[choice(('Alive','Dead','Dead','Dead')) for i in range(size[0][0])] for j in range(size[0][1])] #Randomly populate grid
        self.Grid = [['Dead' for i in range(self.size - 1)] for j in range(self.size-1)]
        for i in [(10,10),(11,10),(11,9),(12,10),(12,11),(10,11),(20,20),(21,21),(19,22),(20,22),(21,22)]:
            self.Grid[i[0]][i[1]] = 'Alive'


    def draw_grid(self):
        '''Draws the cells'''
        Size = self.whole
        for x in range( Size[1] , Size[0][0] , Size[1]):
            for y in range( Size[1] , Size[0][1] , Size[1] ):
                pygame.draw.line(self.screen,(200,200,200),(0,y),(x,y))
                pygame.draw.line(self.screen,(200,200,200),(x,0),(x,y))  

    def draw_to_screen(self):
        for x in range(self.size-1):
            for y in range(self.size-1):
                Cell = self.Grid[x][y]
                pos , size = ( (y * self.whole[1])+2 , (x * self.whole[1])+2 ) , ( self.whole[1]-2 , self.whole[1]-2 )
                if Cell is 'Alive': #Yay!English!                    
                    self.screen.fill((255,255,255),Rect( pos , size ))
                elif Cell is 'Dead':
                    self.screen.fill((0,0,0),Rect( pos , size ))


    def get_neighbors(self,x,y,grid):
        '''Returns the neighbors of a given cell'''
        Neighbors = []
        for a in (-1,1,0):
            for b in (-1,1,0):               
                if a==b and a==0:continue              
                try:Neighbors.append(grid[x+a][y+b])
                except IndexError:continue
        return Neighbors         


    def Implement_Laws(self):  
        '''Enforces the laws of GOL upon the inhabitant cells'''
        New = copy.deepcopy(self.Grid)
        for x in range(self.size-1):
            for y in range(self.size-1 ):
                Cell = self.Grid[x][y]                
                Neighborhood = self.get_neighbors( x , y , self.Grid).count('Alive')
                if Cell is 'Alive':                        
                    if Neighborhood >= 4: #Die of over population                      
                        New[x][y] = 'Dead'
                    elif Neighborhood <= 1: #Die of Loneliness                     
                        New[x][y] = 'Dead'
                    else:
                        New[x][y] = 'Alive'

                elif Cell is 'Dead':
                    if Neighborhood == 3: # Birth of a new cell
                        New[x][y] = 'Alive'
        self.Grid = New

    def Run_Simulation(self,time='inf'):
        '''Runs the Game'''
        clock = pygame.time.Clock()
        while self.time < time:
            for event in pygame.event.get():
                if event.type == QUIT:
                    exit()

            self.draw_to_screen()
            self.Implement_Laws()      

            clock.tick(30)
            self.time += 1

            pygame.display.update()




Size = ((700,700),10)
Game = game_of_life(Size).Run_Simulation()

Image Image

Thaddeus Abiy - 7 years, 4 months ago

I wanted to do a python solution but input images are hard to parse..I was too lazy to input all those grid values..@Chung Gene Keun It would be cool if you could also provide a text file of the input values so it would be easy to parse for all of your problems

Thaddeus Abiy - 7 years, 4 months ago

why the answer is 3 please explain

Kathly Marquez - 7 years, 4 months ago

My solution in javascript with graphical representation: http://pastebin.com/P6qiy5Qv

Alfred Yip - 7 years, 4 months ago
Aditya Mishra
Jan 28, 2014

most of those live cells will die within first to second transition, concentrate only on the most clustered ones. there are 2 groups of 3 adjacent live cells , of those, only the one at the middle of the board will last the longest and yield the lifetime of the group.

the dead cells at row 10,column 11 and the one at row 9,column 12 will become live and the node at row 11,column 11 stays alive in second gen. some more second gen cells will be live but they will die in the 2-3 transition.

after that, all live cells will die except the one at row 11,column 11 which will be resurrected, which will then die in 3-4 transition.

hence ,correct choice is 3.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...