How long will you collide?
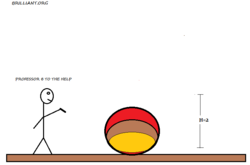 A ball of mass
1
kg
is dropped from a height
H
=
2
m
. Estimate how long the ball is in contact with the ground (in seconds)?
A ball of mass
1
kg
is dropped from a height
H
=
2
m
. Estimate how long the ball is in contact with the ground (in seconds)?
Details and assumptions
-
Simplify the question by modeling the ball as an ideal spring of spring constant
1
0
0
Nm
∣
.
- If necessary, take the gravitational acceleration to be 9 . 8 m/s 2 .
The answer is 0.314.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
I think the answer above is wrong: if you consider this problem is a oscillation problem, the answer above is just a haft time of a full period. We must take the initial value such as velocity of the ball right before hitting the ground, and the original coordination of the system where net force is zero. The answer would be T=(pi+ 2.arccos( squareroot (1/(1+ (mg)^2/2gH.K))) ) . omega
but, the oscillation has to be half the full Time period. Think of it this way, The spring has only been compressed, and not stretched, For a full time period after being compressed it us to be stretched by a certain amount, then return to the make up a full time period.
In your first step , u have applied LAW OF CONSERVATION OF ENERGY without taking into consideration the decrease in GRAVITATION POTENTIAL ENERGY ( mgx)
The answer if u neglect the change in gravitational potential energy will be twice the answer given in the solution i. e T = 2×0.314 = 0.628 But if u consider gravitation potential energ change also im getting T= 0.6751 approximately.
If you consider the ball as a Ideal spring, then the effective mass will be 1/3 not 1.BEcause the mass 1kg becomes the mass of the spring, Not the mass of an object hanging on the end of the spring.
You are right,, though i figured out that such was not the case,,, but the truth is that as u said only 1/3 mass of spring accounts for the question ,,, what should have been said instead was that the ball was attached to a spring (massless) and released,, then answer would be as it is
The system works like a oscillator, and the required time is half period. So:
t = T/2 = pi*sqrt(m/k) ~ 0.314
Let's say the ball just contacted the ground with v 0 at t = 0 . From the eq. of motion m x ¨ + k x = 0 , x ( t ) = v 0 k m sin ( m k t ) . Then, x ˙ ( t ) = 0 when t = 2 π k m . T = π 1 0 0 1 = 1 0 π .
kx=mgh; x=0.196m
v^2=u^2+2aS; v=(39.2)^1/2
t=x/t; hence, t=0.313
The f of spring = sqrt(k/m)/(2 * pi) .... Hence T = (2 * pi)/sqrt(k/m)
But the ball is only compressed, not stretched.
That would take only half the period T...
T/2 = pi/sqrt(k/m) = pi/sqrt(100/1) =. 314
cant we equate the impulsive change in momentum to the net force on the ball ? F= m * delta(v) * t. find t here?
By conservation of energy
2 1 m v 2 + 2 1 K x 2 = 2 1 m v 0 2 .
Where v 0 = 2 g H
Thus
v = d t d x = v 0 2 − m K x 2 .
Solving for t
v 0 2 − ( K / m ) x 2 d x = d t
2 1 T = ∫ 0 x 0 v 0 2 − ( K / m ) x 2 d x = 2 π K m
Where x 0 = v 0 m / K
T = π K m .