How many 10-digit sequence are there?
Find the number of 10-digit sequences where the difference between any two consecutive digits is 1, using only the digits 1, 2, 3, and 4.
Examples of such 10-digit sequences are 1234321232 and 2121212121.
Bonus: Let T ( n ) be the number of such n -digit sequences. What is lim n → ∞ T ( n ) T ( n + 1 ) ?
The answer is 288.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
The meat of the solution is hidden in "Note that".
Nice solution, exactly what i would have written. Is this generalizable using m different "digits" on each digit space (instead of just 4)? I will try to solve that. :)
Both A and B are slight alterations of the Fibonacci sequence, where A(n)=2F(n) and B(n)=2F(n+1), hence T(n) = 2F(n+2)
You can also figure this using a tree diagram. For the numbers starting 1 and 4, there is only one possibility for the result. You will find out for every digit, it goes in a Fibonacci sequence, so for the case of the first digit being 1 and 4, the sequence goes 1 1 2 3 5 8 13 21 34 55, 55 is the number of possible outcomes for the number starting with 1, and 55 is the number of possible outcomes for the number starting with 4. For 2 and 3, since the number of options for the second number is 2, we skip the first number of the Fibonacci sequence, thus leaving us with the 11th number of the Fibonacci sequence, 89 for the number of possibilities for 2, and another 89 possibilities with 3.
Therefore, the number of results is (55+89)*2=288
I found it like that too ! :D
I did that too
Sir, Where is it written that the number should start with 1 0r 4 or end with 1 or 4. Why can't we fix first place by 4 possibilities (1,2,3,4) and so each next term will have 2 possibility (consecutively). 4*2^9=2048. Plz do tell me my mistakes
Log in to reply
If we start with 1 then first digit can be written in 1 way, second digit in 1 way , third digit in 2 ways, fourth digit in 3 ways, fifth digit in 5 ways and so on. Now if we can observe that the pattern follows Fibonacci sequence hence the 10th digit can be written in 55 ways. The same is the case for 4. The case of 2 or 3 is nothing but the same sequence as 1 or 4 starting from 2nd digit of that sequence and adding one more digit at the end which can be written in 89 ways. Hence 2 * (55 + 89) = 288
1 2 3 4 5 6 7 8 9 10 11 12 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 |
|
Log in to reply
I need to learn python, there is no excuse for a mathemtician not to know some programming..
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
|
It looks like Python is popular among users of this site. Someone has even made a Python script to brute force any problem on this site.
https://5f3759df.wordpress.com/2018/02/21/extracting-answers-to-problems-from-brilliant-org/
We can work out the number of sequences ending with a specific digit by adding together the number of sequences up to the previous number which ends with a number adjacent to the desired number.
For example, by using the tree diagram below (considering only the sequences starting with a 1), we can see that the number of 6-digit sequences ending in 2
(
5
)
is equal to the number of 5-digit sequences ending in 1
(
2
)
added to the number of sequences ending in 3
(
3
)
:
 This is applicable down to just 2-digit sequences: the number of 2-digit sequences ending in 3
(
2
)
is equal to the number of 1-digit sequences ending in either 2
(
1
)
, or 4
(
1
)
. In this case, these two sequences are
2
,
3
and
4
,
3
respectively.
This is applicable down to just 2-digit sequences: the number of 2-digit sequences ending in 3
(
2
)
is equal to the number of 1-digit sequences ending in either 2
(
1
)
, or 4
(
1
)
. In this case, these two sequences are
2
,
3
and
4
,
3
respectively.
With this information, starting with the 4 possible 1-digit sequences, we can work out the number of sequences of successive lengths ending in each digit:
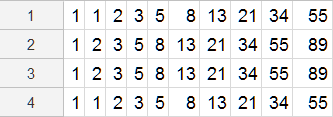 And now we can work out the total number of 10-digit sequences using
5
5
+
8
9
+
8
9
+
5
5
=
2
8
8
And now we can work out the total number of 10-digit sequences using
5
5
+
8
9
+
8
9
+
5
5
=
2
8
8
For the bonus question: with the table above, we can see the Fibonacci sequence emerging as the length of the sequence increases. Because the ratio between successive numbers in the Fibonaccio sequence tends towards the golden ratio ( ϕ ) , we can see that, as the above sequence increases in length:
T ( n + 1 ) 1 + T ( n + 1 ) 2 + T ( n + 1 ) 3 + T ( n + 1 ) 4 = ϕ T ( n ) 1 + ϕ T ( n ) 2 + ϕ T ( n ) 3 + ϕ T ( n ) 4
T ( n + 1 ) 1 + T ( n + 1 ) 2 + T ( n + 1 ) 3 + T ( n + 1 ) 4 = ϕ ( T ( n ) 1 + T ( n ) 2 + T ( n ) 3 + T ( n ) 4 )
T ( n + 1 ) = ϕ T ( n )
T ( n ) T ( n + 1 ) = ϕ ≈ 1 . 6 1 8
The 1 -digit possibilities are 1 , 2 , 3 , and 4 ; for a total of 4 different sequences.
For 2 -digit possibilities, the first digit can be 1 , 2 , 3 , or 4 . If the first digit is 1 , then the second digit must be 2 . If the first digit is 2 , the the second digit must be 1 or 3 . If the first digit is 3 , then the second digit must be 2 or 4 . And if the first digit is 4 , then the second digit must be 3 . The possible sequences are 1 2 , 2 1 , 2 3 , 3 2 , 3 4 , and 4 3 - 1 starting with 1 , 2 starting with 2 , 2 starting with 3 , and 1 starting with 4 - for a total of 1 + 2 + 2 + 1 = 6 different sequences for 2 digits.
For 3-digit possibilities, the first digit can be 1 , 2 , 3 , or 4 . If the first digit is 1 , then the second digit must be 2 , and from above we know that there are 2 2 -digit possibilities that start with 2 , so there are 2 3 -digit possibilities that start with 1 . If the first digit is 2 , then the second digit must be 1 or 3 , and from above we know that there is 1 2 -digit possibility that starts with 1 and 2 2 -digit possibilities that start with 3 , for a total of 1 + 2 = 3 3 -digit possibilities that start with 2 . If the first digit is 3 , then the second digit must be 2 or 4 , and from above we know that there are 2 2 -digit possibilities that start with 2 and 1 2 -digit possibility that starts with 4 , for a total of 2 + 1 = 3 3 -digit possibilities that start with 2 . If the first digit is 4 , then the second digit must be 3 , and from above we know that there are 2 2 -digit possibilities that start with 3 , so there are 2 3 -digit possibilities that start with 4 . There are then a total of 2 + 3 + 3 + 2 = 1 0 different sequences for 3 digits.
Now we can see a recursive pattern. Let a n be the number of n -digit possibilities that start with 1 or 4 , b n be the number of n -digit possibilities that start with 2 or 3 , and t n be the total number of n -digit possibilities. Then using the above arguments, a n = b n − 1 , b n = a n − 1 + b n − 1 , and t n = 2 ( a n + b n ) . Then substituting a n = b n − 1 and b n = a n − 1 + b n − 1 , we have t n = 2 ( b n − 1 + a n − 1 + b n − 1 ) , and substituting b n − 1 = a n − 2 + b n − 2 , we have t n = 2 ( a n − 2 + b n − 2 + a n − 1 + b n − 1 ) , and since t n − 1 = 2 ( a n − 1 + b n − 1 ) and t n − 2 = 2 ( a n − 2 + b n − 2 ) , we have t n = t n − 2 + t n − 1 .
From above we know that t 1 = 4 and t 2 = 6 , and so using t n = t n − 2 + t n − 1 we can find the first 1 0 terms of the sequence to be 4 , 6 , 1 0 , 1 6 , 2 6 , 4 2 , 6 8 , 1 1 0 , 1 7 8 , and 2 8 8 , which means t 1 0 = 2 8 8 .
Bonus: Since t n = t n − 2 + t n − 1 , it has the same recursive pattern as the Fibonacci sequence, and so lim n → ∞ t n t n + 1 = ϕ ≈ 1 . 6 1 8 .
C#
using System;
namespace ConsoleApp1
{
class Program
{
static int Count = 0;
static long Max = (long)Math.Pow(10,9);
static void Expand(ref long _value)
{ if (_value > Max)
Console.WriteLine($"[{++Count}]\t{_value}"); // branch finished
else
{ long _tmp;
short _lastDigit = (short)(_value % 10);
long _root = 10 * _value + _lastDigit;
if (_lastDigit > 1) { _tmp = _root - 1; Expand(ref _tmp); }
if (_lastDigit < 4) { _tmp = _root + 1; Expand(ref _tmp); }
}
}
static void Main(string[] args)
{ for(long k = 1; k<=4; k++) Expand(ref k);
Console.WriteLine($"Count: {Count}");
}
}
}
Noting that any number must go even, odd, even, or vise versa. We can treat 1 and 4 as end points, E, and 2 and 3 as middle points, M. (Where 2 E's cannot be next to each other). (Note we are now counting precisely half of total, as we can choose the first digit to be odd or even.)
Let F(n) be the number of combinations of E and M. For n>2,
F(n)= (first digit E, 2nd digit M) F(n-2) + (first digit M) F(n-1)
F(1)=2 (E, M)
F(2)=3 (EM, ME, MM)
We can deduce that F(n) = (n+2)th Fibonacci number, f(n+2). So F(10)=144. So T(10)=288.
Extra: lim(n -> infinity) T(n+1)/T(n) = lim(n -> infinity) f(n+3) / f(n+2) = phi
Let T ( n ) be the number of such n -digit sequence.
Let A ( n ) be the number of such n -digit sequence that end in either 1 or 4.
Let B ( n ) be the number of such n -digit sequence that end in either 2 or 3.
Now T ( n ) = A ( n ) + B ( n ) .
Note that A ( n + 1 ) = B ( n ) and B ( n + 1 ) = B ( n ) + A ( n ) = B ( n ) + B ( n − 1 ) . Since A ( 1 ) = 2 , B ( 1 ) = 2 , we can construct the following table, using the mentioned recursive relation, and obtain the answer.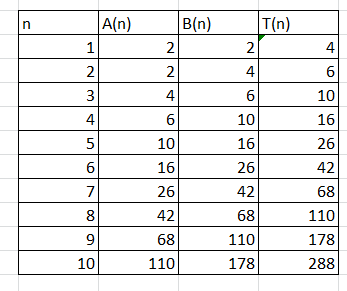
For the bonus question: n → ∞ lim T ( n ) T ( n + 1 ) = n → ∞ lim A ( n ) + B ( n ) A ( n + 1 ) + B ( n + 1 ) = n → ∞ lim B ( n − 1 ) + B ( n ) B ( n ) + B ( n + 1 ) = n → ∞ lim B ( n + 1 ) B ( n + 2 ) = . . . = ϕ ≈ 1 . 6 1 8 0 3