How many a's are there?

Case 1: a < 0

In this case, $(e^x-a)$ will always be positive. However, the other term $(3ax+1)$ will be negative when $x > -\frac{1}{3a}$ . So, $f(x)$ cannot be nonnegative for all real values of $x$ . Thus, there is no solution when $a < 0$ .

Case 2: a = 0

The function reduces to $f(x) = e^x$ . And, $e^x > 0$ for all values of $x$ . Therefore, $a = 0$ is a valid option which satisfies the given condition.

Case 3: a > 0

We see that, $(e^x-a)$ is negative when $x < \ln a$ , zero when $x = \ln a$ , and positive when $x > \ln a$ . Similarly, $(3ax+1)$ is negative when $x < -\frac{1}{3a}$ , zero when $x = -\frac{1}{3a}$ , and positive when $x > -\frac{1}{3a}$ . If there is an interval between $\ln a$ and $-\frac{1}{3a}$ , we find that one term is going to be positive and another negative. This arrangement makes $f(x)$ negative. So, there cannot be any gap between $\ln a$ and $-\frac{1}{3a}$ for $f(x)$ to be always nonnegative. Hence, acceptable values of $a$ need to satisfy the equation $\ln a = -\frac{1}{3a}$ .

The equation $\ln a = -\frac{1}{3a}$ has two solutions. These are $a \approx 0.2204, 0.5384$ .

This question is interesting but somewhat computationally tedious.

For a product of two functions to always be positive, both functions must be negative at the same time and positive at the same time. Since both are continuous, according intermediate value theorem they must have roots at the same value of x. Since both functions are monotone increasing, around these roots, their signs must be identical.

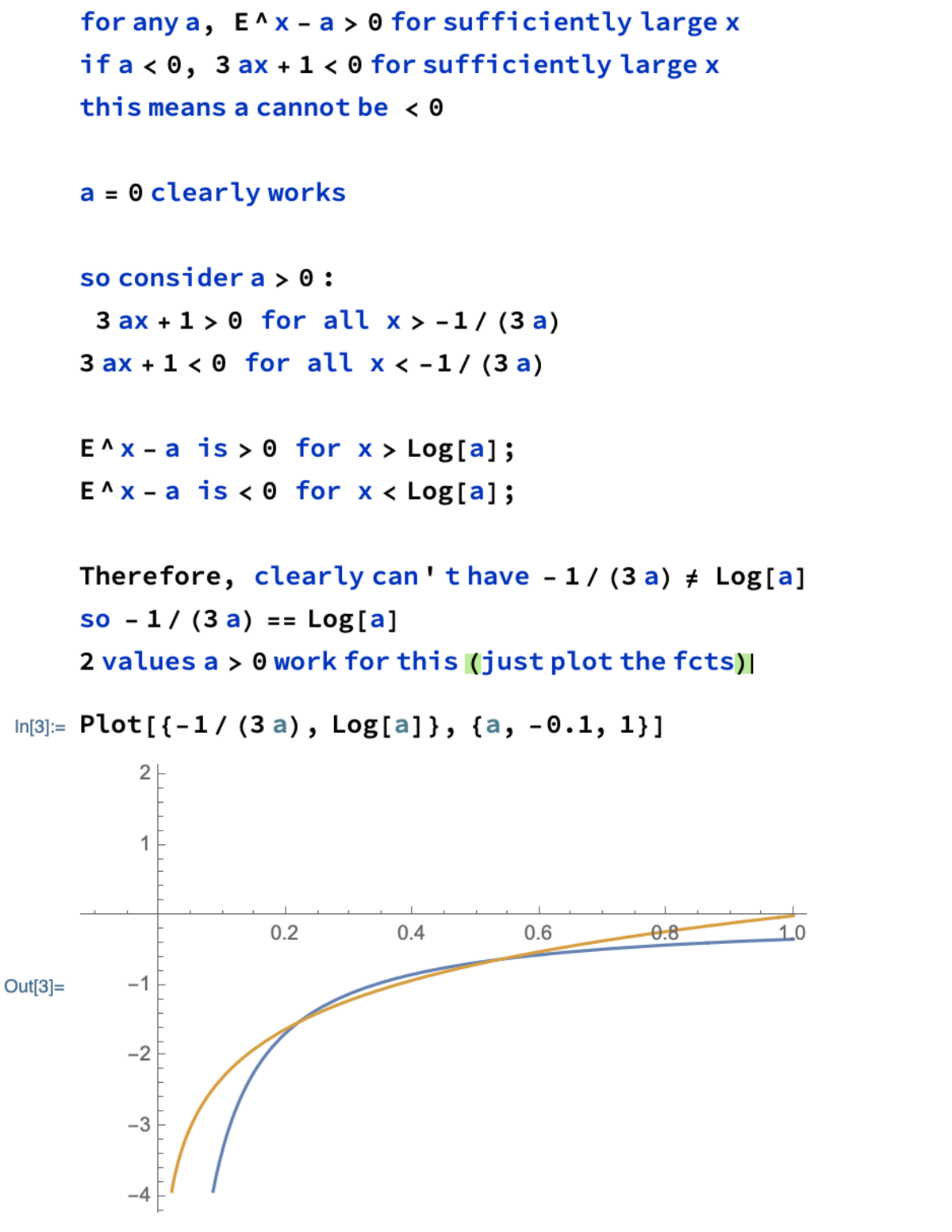
We see that $0 = 3ax + 1$ implies $x = -1/3a$ and so we want $a$ such that $a = e^{-1/3a}$ . This equation is transcendental; forcing students to use direct computational methods to gain any insight as to how many solutions exist.

On a math contest it would be better to write questions which allow students to more easily visualize the solutions to such tricky equations- perhaps $e^x = x$ or something related to that would simplify it enough to avoid the use of a table of values, or other brute force tools.

However I think this is a very interesting way to bring up the intermediate value theorem. I look forward to other problems you come up with!