How many bounces can you find?
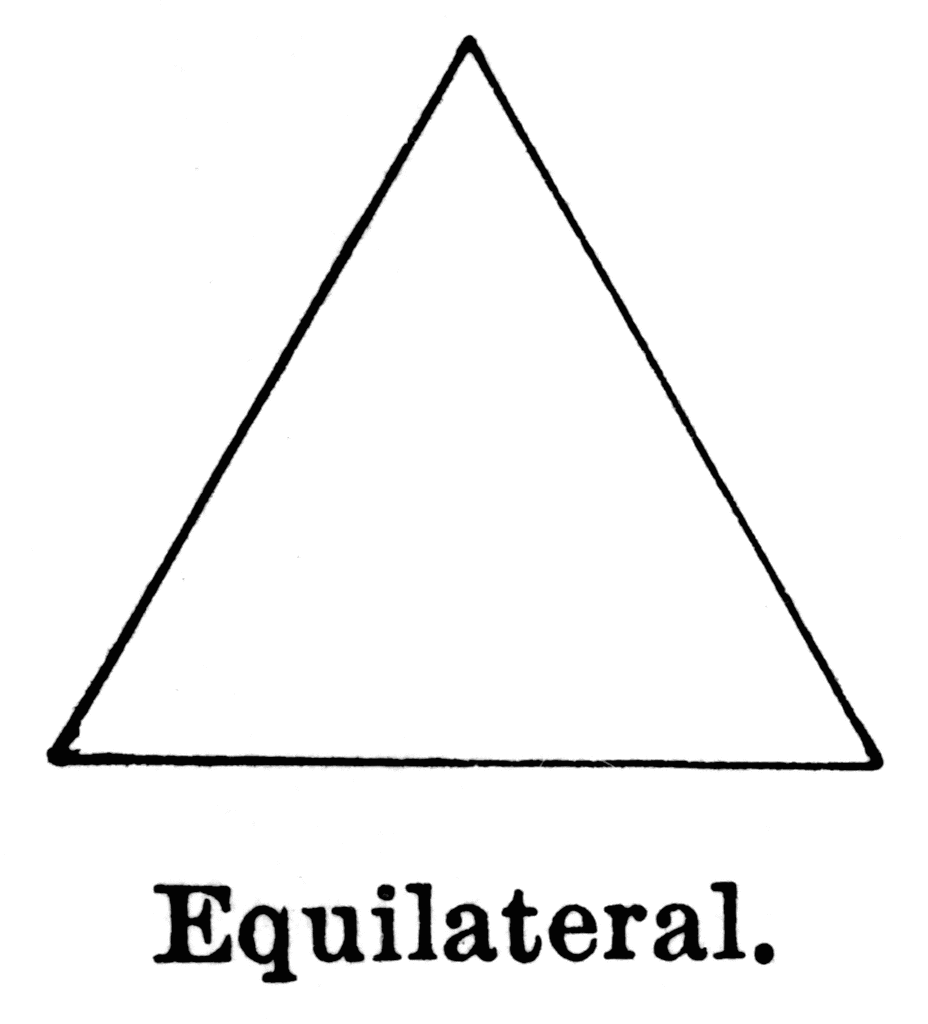
Suppose you're bouncing a ball around a unit equilateral triangle, starting on one of the sides. The angle of incidence equals the angle of reflection, and the ball cannot hit any vertices.
Let's call a cycle any way of bouncing the ball such that after a finite number of bounces it reaches the starting point. A cycle ends when it reaches the starting point.
Given that the total length of the cycle is less than or equal to (that is, that total distance it travels before reaching the starting location), what is the maximum number of bounces in the cycle?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!