How many cards for a Flush?
You shuffle a standard deck of cards, draw the top card, and place it on the table. You keep doing this until you can form a flush from the cards you have drawn.
What is the expected number of cards you will draw (rounded to the nearest integer)?
Note: A standard deck of cards has 52 cards in total, with 4 different suits. A flush is formed when there are 5 cards of the same suit.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
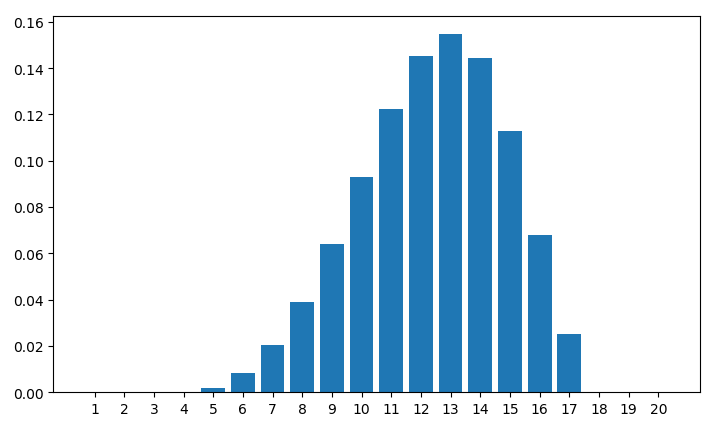
I used your formulas to compute the probability distribution of the number of cards that have to be drawn to form a flush.
Log in to reply
Why 17 is not the answer? Since Drawing 17 cards assures a flush
Log in to reply
We are talking about probability here. You will certainly have drawn a flush after 1 7 cards, but you might have drawn a flush after just 5 cards. There are different probabilities for the number of cards it takes to drawn a flush (see the graph above), and the expected value of the associated random variable is slightly greater than 1 2 .
This is a calculation like asking what the expected value obtained after rolling a die. Each of the values 1 , 2 , 3 , 4 , 5 , 6 occurs with probability 6 1 , and so the expected value is 6 1 ( 1 + 2 + 3 + 4 + 5 + 6 ) = 3 . 5
Another simple approach... 5card flush from say 10 cards... Then no of flush combinations is C(10,5)=252. Probability each flush is (1/4)^5.=1/1024 (this is actually probability of 5 or more cards of same suite). Then Probability all flush combinations =252/1024.=24.6% Using same approach For 11 cards flush probability 45% For 12 cards flush probability 77%. ANSWER 12 cards.
Log in to reply
The probability of any particular flush is not ( 4 1 ) 5 - that would be the probability if the cards were replaced in the pack each time. We are interested in the probability of getting a flush when the cards are dealt without replacement.
You also seem to be assuming that the mean (expectation) of the distribution is the same as the mode of the distribution. This is not true, since (as the graph below shows) the mode is 1 3 .
This will not be an exact solution, but more of an educated guess. But maybe it is still valuable for people to get a feeling for probability. The minimum number of cards you need to draw for a flush is obviously 5. The maximum number is 17. Because if you haven't hit a flush with 16 cards, it means you have 4 cards of each color. Therefore the 17th card has to complete one flush. Now the average of 5 and 17 is 11. But since the distribution of probability in a situation like this (drawing something with a probability lower than 1/2 from a large set) is typically shifted towards the right, 12 is a good guess. Especially considering the possible choices.
I decided to ignore the deck part of the problem, and just assume an infinite “shoe”. I wrote a little program, using some of the symmetries in the probability tree, so I didn’t have to deal with a billion nodes or so.
The answer I came up with was 11.736762030050159.
Log in to reply
I guess that "infinite shoe" is the same as "selection with replacement". That would make things a lot easier, and explain why your calculated answer was smaller than the true value.
Here is some quick python code implementing Mark brilliant solution :
1 2 3 4 5 6 7 8 9 |
|
I wrote a bit of code in processing to simulate drawing cards and ran it 100,000,000 times to get 12.359815. With this method the number of cards needed for a flush, the number of suits and the number of cards in a suit are each variables so it could be worked out for other variations. I know there's undoubtedly better and more elegant solutions in both code and concept but this worked for me. I should probably have a go at Python though.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 |
|
Not a solution
Let me define some questions as,
Q 5 What is the probablity of forming exactly one flush on your 5th pick?
Q 6 What is the probablity of forming exactly one flush on your 6th pick?
..
Q 1 7 What is the probablity of forming exactly one flush on your 17th pick? (since 17th pick guarantees the flush)
And the answers of these questions as A 5 , A 6 , . . . , A 1 7 , respectively
So finally our answer will be 5 × A 5 + 6 × A 6 + . . . + 1 7 × A 1 7 ≈ 1 2
I found that
| Answers | Probabilities |
| A 5 | 0.00198 |
| A 6 | 0.00986 |
| A 7 | 0.02851 |
| A 8 | 0.06251 |
| A 9 | 0.11509 |
| A 1 0 | ? |
| A 1 1 | ? |
.. ..
But I could not find a formula for A 1 0 to A 1 7
If we get a flush on the 5th pick we are done so your questions and answers need revising.
Your Q6 should really be: What is the probability of not forming a flush on the 5th pick, but forming one on your 6th.
The actual A6 is your A6-A5.
Let E a , b , c , d be the expected number of additional cards that have to be drawn to obtain a flush, given that a Spades, b Hearts, c Diamonds and d Clubs have already been drawn. Conditioning on the outcome of the next draw, we see that E a , b , c , d = 1 + 5 2 − ( a + b + c + d ) ( 1 3 − a ) E a + 1 , b , c , d + ( 1 3 − b ) E a , b + 1 , c , d + ( 1 3 − c ) E a , b , c + 1 , d + ( 1 3 − d ) E a , b , c , d + 1 0 ≤ a , b , c , d ≤ 4 and we also have that E a , b , c , d = 0 when any one of a , b , c , d is equal to 5 or more. It is a simple matter to plug this recursive relation into a computer programme, and obtain the expected number of draws to obtain a flush as E 0 , 0 , 0 , 0 = 1 2 . 3 5 9 8 0 1 6 making the answer 1 2 .
Trying a little harder, we note that, if we define F a , b , c , d = ( 1 3 − a 1 3 − b 1 3 − c 1 3 − d 5 2 − a − b − c − d ) E a , b , c , d where ( p q r s p + q + r + s ) is the multinomial coefficient ( p q r s p + q + r + s ) = p ! q ! r ! s ! ( p + q + r + s ) ! then we have the recurrence relation F a , b , c , d = ( 1 3 − a 1 3 − b 1 3 − c 1 3 − d 5 2 − a − b − c − d ) + F a + 1 , b , c , d + F a , b + 1 , c , d + F a , b , c + 1 , d + F a , b , c , d + 1 for 0 ≤ a , b , c , d ≤ 4 , and hence F 0 , 0 , 0 , 0 = a , b , c , d = 0 ∑ 4 ( 1 3 − a 1 3 − b 1 3 − c 1 3 − d 5 2 − a − b − c − d ) N a , b , c , d where is N a , b , c , d is the number of ways of getting from ( 0 , 0 , 0 , 0 ) to ( a , b , c , d ) by taking steps of size 1 in any one of the components at any one time. In other words, N a , b , c , d = ( a b c d a + b + c + d ) and hence F 0 . 0 . 0 . 0 = a , b , c , d = 0 ∑ 4 ( 1 3 − a 1 3 − b 1 3 − c 1 3 − d 5 2 − a − b − c − d ) ( a b c d a + b + c + d ) = 6 6 3 0 3 8 3 1 6 8 9 8 8 2 0 1 8 8 6 7 9 6 3 1 6 0 0 0 0 0 To obtain E 0 , 0 , 0 , 0 , we need to divide this by ( 1 3 1 3 1 3 1 3 5 2 ) = 5 3 6 4 4 7 3 7 7 6 5 4 8 8 7 9 2 8 3 9 2 3 7 4 4 0 0 0 0 obtaining E 0 , 0 , 0 , 0 = 9 4 9 8 1 8 1 5 4 0 4 1 1 7 3 9 5 6 3 9 6 1 8 5 = 1 2 . 3 5 9 8 0 1 6 2
Yet another approach! For any 0 ≤ a , b , c , d ≤ 1 3 , the probability p a , b , c , d = ( 1 3 1 3 1 3 1 3 5 2 ) ( a b c d a + b + c + d ) ( 1 3 − a 1 3 − b 1 3 − c 1 3 − d 5 2 − a − b − c − d ) is the probability that, when a pack is dealt, the first a + b + c + d cards consist of a Spades, b Hearts, c Diamonds and d Clubs. If N is the number of cards that have to be dealt to obtain a flush, then P [ N ≥ k + 1 ] is the probability that there is no flush in the first k cards, and hence P [ N ≥ k + 1 ] = { ∑ a + b + c + d = k 0 ≤ a , b , c , d ≤ 4 p a , b , c , d 0 0 ≤ k ≤ 1 6 k ≥ 1 7 and hence E [ N ] = k ≥ 0 ∑ P [ N ≥ k + 1 ] = k = 0 ∑ 1 6 a + b + c + d = k 0 ≤ a , b , c , d ≤ 4 ∑ p a , b , c , d = a , b , c , d = 0 ∑ 4 p a , b , c , d = E 0 , 0 , 0 , 0 retrieving the previous result.