How Many Colors Do You Need?

Probability Level 2

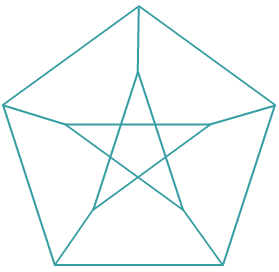
The figure above is partitioned into 11 regions. What is the fewest number of colors needed to paint each region so that no two regions which share an edge also share the same color?

3 4 5 2

3 solutions

Eli Ross Staff
Sep 18, 2015

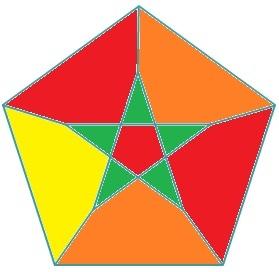
If we try to color the regions with 3 colors by making necessary choices for the regions one-by-one, we see that it is impossible:

On the other hand, it is quite easy with 4 colors. Here's an example of such a coloring:

In fact, any separation of the plane into contiguous regions can be colored such that no adjacent regions have the same color in using at most four colors . This is known as the "four color theorem".

I don't think this reasoning works as listed because in going from the 3rd diagram to the 4th, the "1" is not a necessary choice. It could also be a "2" because the only EDGE taken so far is the adjoining "3". That triangle connects to the adjacent "2" via a vertex, not an edge. Same reasoning applies between the 5th and 6th and the 7th and 8th diagrams. It seems using this method would entail a more complicated "tree" test, trying out each possibility until all have been exhausted. Am I missing something?

Jeff Wiseman - 4 years, 8 months ago

I just directly applied "Four colour theorem" without reading the entire problem.

Satyajit Mohanty - 5 years, 8 months ago

Then you might get tricked if a) the map is actually colorable in three colors, or b) it is on a torus or some even more complicated surface.

Ivan Koswara - 5 years, 8 months ago

I agree with Jeff Wiseman that this argument is missing something.

Here's how I thought through it. We use colors 1,2,3 and see what is forced. The outermost 5 regions must be colored in the pattern 1,2,3,2,3 (in the dual, it is an odd cycle so needs all three colors, and a 5-cycle has a unique coloring up to symmetry). In three of the star points then we are forced to use color 1. The center then is either 2 or 3, and we may use 2 by symmetry. But then one of the last star points has all three colors in its neighborhood.

Ben Reiniger - 4 years, 5 months ago

Artur Toledo
Sep 21, 2015

Saswat24 Das
Sep 19, 2015

The maximum No. of figures one of the Figure is touching = 3 . Clearly the no. of colors we need = $\boxed{4}$

Esta errada esta resposta, tem 12 regiões, pode procurar que vai encontrar

Ezequiel Gregorio - 4 years, 8 months ago

How Many Colors Do You Need?

3 solutions

0 pending reports